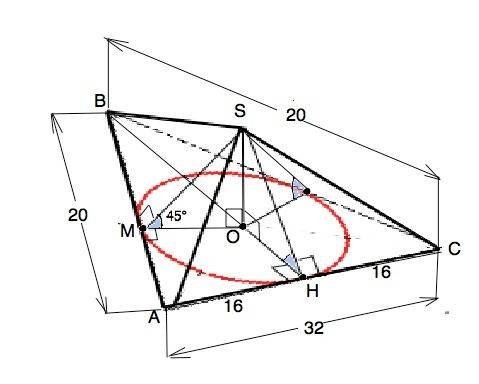
Формула объема пирамиды V=H•S•1/3. Площадь основания S=h•a. По условию ∆ АВС равнобедренный, поэтому его высота ВН является медианой и биссектрисой. АН=СН=16 см. Из ∆ АВH по т.Пифагора ВН=√(AB²-AH²)=√(20²-16²)=12 см. ⇒ S=12•32:2=192 см² .
Углы между плоскостью основания и каждой из боковых граней равны 45°, значит, высоты боковых граней ( наклонных) и их проекции на плоскость основания перпендикулярны ребру при основании и образуют линейный угол двугранного угла=45°. Высоты боковых граней равны между собой. Их проекции равны радиусу r вписанной окружности. r=S:p, где S - площадь треугольника, р - его полупериметр. Из суммы длин сторон треугольника р=(2•20+32):2=36 см.⇒ r=192:36=16/3 см. Треугольники, образованные высотой пирамиды SO, радиусом вписанной окружности и высотой боковой грани - прямоугольные равнобедренные ( угол МSO=SMO=45°, следовательно, SO=МО=НО=16/3. V(SABC)=(1024/3192•16/3):3=1024/3 см³
Sавсд=АД*ВН
Sавсд=12*5=60
Sавсд= АД*ВН=АВ*СН1
АВ*СН1=АД*ВН=60
АВ*СН1=60
10*СН1=60
СН1=6