Здравствуйте!
Для того чтобы найти недостающие углы трапеции, мы можем воспользоваться свойством суммы углов в многоугольнике.
Согласно этому свойству, сумма всех внутренних углов в многоугольнике равна сумме двух прямых углов, то есть 180°.
В нашем случае у нас уже известны два угла трапеции: 152° и 56°. Давайте обозначим остальные два угла буквами X и Y.
Таким образом, уравнение для суммы углов трапеции будет таким: 152° + 56° + X + Y = 180° (сумма всех углов трапеции равна 180°).
Теперь решим это уравнение:
152° + 56° + X + Y = 180°
Сложим известные углы:
208° + X + Y = 180°
Выразим X + Y:
X + Y = 180° - 208°
X + Y = -28°
Таким образом, сумма недостающих углов X и Y равна -28°.
Причина такого ответа заключается в том, что в данном случае нет возможности найти конкретные значения для недостающих углов без дополнительной информации или дополнительных свойств трапеции.
Поэтому в данном случае мы можем сказать, что недостающие углы трапеции равны между собой и их сумма равна -28°.
Надеюсь, ответ был понятен и объяснение было подробным! Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их.
Для решения этой задачи, давайте начнем с построения треугольника, серединами сторон которого являются точки А, В и С.
1. Задачу мы можем решить, используя свойство медиан треугольника. Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
2. Для начала, построим отрезки, которые будут являться медианами треугольника. Медиана из вершины А будет соединять вершину А с серединой стороны ВС. Медиана из вершины В будет соединять вершину В с серединой стороны АС. Медиана из вершины С будет соединять вершину С с серединой стороны AB.
3. Чтобы найти середину стороны треугольника, нужно соединить две точки, являющиеся концами этой стороны и провести серединный перпендикуляр. Найдем середину стороны ВС. Для этого проведем прямую, перпендикулярную стороне ВС, через точку В. Аналогично найдем середины сторон AC и AB. Обозначим их точками D, E и F соответственно.
4. Теперь соединим полученные точки А, B и С линиями. Мы получили треугольник ABC, серединами сторон которого являются точки D, E и F.
Теперь перейдем к заданию Е, которое требует закрасить все точки квадрата ABCD, расстояние до которых от вершины В не меньше стороны этого квадрата.
1. Найдем расстояние от вершины В до одной из сторон квадрата ABCD. Заметим, что сторона квадрата AB совпадает с отрезком ВD. Следовательно, сторона квадрата ABCD равна длине отрезка ВD.
2. Чтобы найти все точки квадрата ABCD, расстояние до которых от вершины В не меньше стороны этого квадрата, нужно закрасить все точки внутри квадрата, а также все точки на его границе.
3. Теперь, найдем точки, которые лежат на границе этого квадрата ABCD. Границы квадрата ABCD образуют стороны этого квадрата и отрезки, соединяющие середины соседних сторон.
4. Закрасим точки внутри квадрата ABCD, а также точки на его границе, используя найденные отрезки и линии.
На рисунке видно, что закрашены точки внутри квадрата ABCD, а также точки на его границе, расстояние от которых до вершины В не меньше стороны этого квадрата.
Таким образом, мы успешно нашли треугольник, серединами сторон которого являются точки А, В и С, и закрасили все точки квадрата ABCD, удовлетворяющие условию задания Е.
Дано :
Точка О - центр окружности.
Радиус окружности = 11 см.
Отрезок МР - хорда, МР = 7 см.
Найти :
Если мы соединим точки О и М ; О и Р, то мы получим радиусы ОМ и ОР соответственно (по определению радиусов окружности).
ОМ = ОР = 11 см, так как радиусы одной окружности равны.
Периметр - это сумма длин всех сторон.Тогда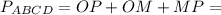
11 см + 11 см + 7 см = 29 см.
29 см.