Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.
Объяснение:
Рисунок прилагается.
Дано: ABC прямоугольный треугольник, ∠ С = 90°, CH- высота, AH = 2 см - проекция катета AC на гипотенузу, BH = 18 см - проекция катета BC на гипотенузу.
Найти катеты AC и BC.
Обозначим для удобства катеты AC = a, BC = b, проекции катетов AH = a₁, BH = b₁, высоту CH = h.
Высота в прямоугольном треугольнике, опущенная на гипотенузу, равна среднему пропорциональному проекций катетов на гипотенузу.
h² = a₁*b₁ = 2 * 18 = 36; h = 6
⇒ Высота треугольника, опущенная на гипотенузу CH = h = 6 см.
Из прямоугольного ΔACH по теореме Пифагора:
a² = h² + a₁² = 6² + 2² = 36 + 4 = 40; a = √40 = 2√10
Катет AC = 2√10 см/
Из прямоугольного ΔBCH по теореме Пифагора:
b² = h² + b₁² = 6² + 18² = 36 + 324 = 360; b = √360 = 6√10
Катет BC = 6√10 см.
Катеты данного прямоугольного треугольника равны 2√10 см и 6√10 см.

В равнобедренной трапеции боковые стороны равны,поэтому равны и углы при основаниях.Сумма боковых углов,односторонних равна 180 °,поэтому 268 °-это сумма тупых углов при основании.Сумма всех углов трапеции равна 360°.
Найти меньший угол трапеции можно двумя
1)Из суммы всех углов 360° вычесть суммы тупых углов 268° и разницу разделить на 2 (угла):
2)Сумма боковых углов,односторонних равна 180 °,в условии-тупые углы при основаниях и их сумма равна 268°.
Один угол равен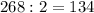 °.
°.
ответ:меньший угол трапеции равен 46 °.