Чертеж к решению - во вложении.
Известно, что биссектрисы двух непротивоположных углов параллелограмма пересекаются под прямым углом и отсекают равнобедренные треугольники. Таким, образом, треугольники АВК и МСД равнобедренные, а треугольник КРМ - прямоугольный.
Все равные углы (накрест лежащие и вертикальные), а также равные отрезки отмечены на чертеже.
Ведем обозначения: ВК=КМ=МС=х, КР=у, МР=z.
Периметр параллелограмма P=2(АВ+ВС)=8х.
Треугольники РАД и РКМ подобны по двум углам. Поэтому
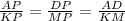
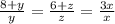
1) 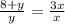
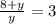
3y=8+y
y=4,
2) 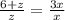
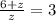
z+6=3z
z=3,
По теореме Пифагора в треугольнике КРМ
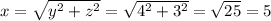
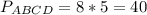
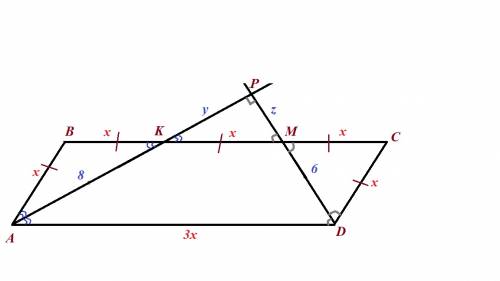
ответ: 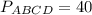
Пусть АВСД-равнобедренная трапеция. АС=10-диагональ, Угол САД=60.
Опустим из вершины С высоту СН к стороне АД. В прямоугольном треугольнике АСН угол АСН=180-угол СНА (=90, та как СН-высота)-угол САН(он же САД)=180-90-60=30. Против угла в 30 градусов лежит катет АН равный половине гипотенузы АС. АН=10/2=5. По теореме Пифагора найдем высоту СН=АС в квадрате-АН в квадрате все под корнем=10 в квадрате-5 в квадрате все под корнем=5 корней из 3. В равнобедренной трапеции высота (СН=5 корней из 3) равна полусумме оснований. А площадь равна произведению полусуммы оснований на высоту. S=5 корней из 3*5корней из 3=75