1. Г
2. Угол DCE = 15°, значит угол ЕСО = 45° - 15° = 30°. В прямоугольном треугольнике ЕОС: sin ECO = OE:CE = sin 30 = 1:2. ответ: 1:2
3. Вписанный угол ABC равен половине центрального AOC ответ: 50°
4. Чтобы ромб был квадратом необходимо чтобы его диагонали были равны, а значит были равны и половины диагоналей. ответ: 8см
5. Зная стороны, найдём длину диагонали:
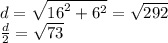
Опустим высоту из центра прямоугольника на сторону с длиной 6. У нас образовался прямоугольный треугольник с катетом 3 см и гипотенузой sqrt(73), можем найти высоту(расстояние от центра до стороны). Оно равно
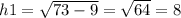
Подходит только вариант А
6. Найдём длину оставшегося катета:
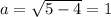
Значит наименьший острый угол лежит напротив катета a, т.к. 1 < 2 (меньший угол лежит напротив меньшего катета). Найдём тангенс:
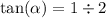
10 и 8 стороны
Объяснение:
Если одна сторона 10, а площадь 64, то высота 6.4см
Если провести эту высоту то образуется прямоугольный треугольник. Косинус его угла 0.6. Косинус это отношение прилежащего катета к гипотенузе. Но нам известен только противолежащий катет. По основному тригонометрическому тождеству найдем синус. Пусть этот угол a.
cos²a + sin²a = 1
0.36 + sin²a = 1
sin²a = 0.64
sina = 0.8 (-0.8 опускаем, т.к в данном случае синус не может быть отрицательным)
Тогда гипотенуза равна 8см. Это и есть вторая сторона.
20
Объяснение:
Примем коэффициент пропорциональности отрезков, на которые боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности, за х, а основание - за у.
Тогда периметр треугольника равен 2*(2х+7х) + у = 110.
По свойству точки касания 2х = у/2 или у = 4х (так как треугольник равнобедренный).
Подставим эту зависимость в первое уравнение.
2*9х + 4х = 110,
22х = 110,
х = 110/22 = 5.
Отсюда находим стороны треугольника:
- боковые стороны равны 2*5+7*5 = 10 + 35 = 45,
- основание равно 110 - 2*45 = 110 - 90 = 20.