Найти длину стороны куба, если диагональ его грани равна 5
ответ: 5√2 /2.
Объяснение: Каждая грань кубы является квадратом
Если длина ребра (стороны) куба a , то длина диагонали грани
будет a√2 (по теореме Пифагора: d² = a² +a² ; d² = 2a² ; d =a√2 )
5 = a√2 ⇒ a = 5 /√2 = 5√2 /2.
Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а) 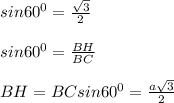
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
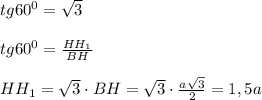
в) Найти площадь боковой поверхности - самая простая часть этого задания:
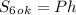 , где
, где 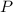 и
и  - периметр основания и высота пераллелепипеда соответственно.
- периметр основания и высота пераллелепипеда соответственно.

г) 
квадрат диагонали грани куба, т.е. квадрат диагонали квадрата равен сумме квадратов двух его смежных сторон. если сторона квадрата х, то 2х²=25
х=5/√2=5√2/2
ответ 5√2/2