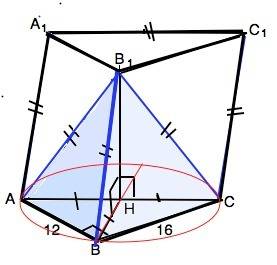
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
4 задача =
x-один из равных углов треугольника
x-второй из равных углов треугольника
y-третий угол треугольника
x+x+y=180
x=y+96
2x+x+96=180
x=28
5 задача = 1)угол А= угол С=60, а сумма углов треугольника равна 180 градусов, следовательно, угол В=60.
2)Итак, все углы по 60 градусов, значит, треугольник АВС - равносторонний, т.е. АВ=ВС=АС.
3)По условию ВС+АС=4, из пункта 2 следует, что АВ=ВС=АС=2 см. Периметр АВС=2+2+2=6 см
6 задача =
Треугольники равны по третьему признаку (по трем сторонам), следовательно, углы у них тоже будут равны. Следовательно, угол ABC = TPK, BAC = PTK, ВСА = PKT. Найдем PKT:
PKT = 180-(TPK+PTK); PKT = 180-(124+46); PKT = 10
Объяснение:
Объяснение:
Если внешний угол при вершине A равен 120°, то внутренний равен 180° - 120° = 60°. AB = BC ⇒ ΔABC - равнобедренный, ⇒ ∠A = ∠C = 60°.
∠B = 180° - 2 * 60° = 60°
∠A = ∠B = ∠C = 60° ⇒ ΔABC - равносторонний.
ч. т. д.