Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
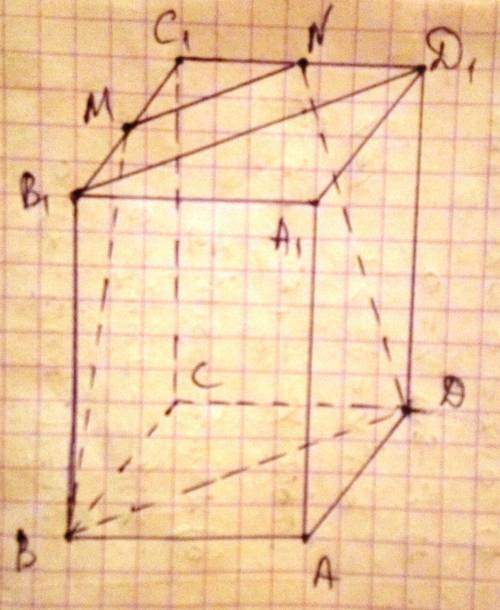
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
ответ: угол А=51°, угол В=39°
Объяснение: обозначим вершины треугольника А В С, высоту СН, биссектрису СК. Рассмотрим полученный ∆СНК. Он прямоугольный, угол СНК=90°, угол КСН=6°, по условиям. Зная что сумма острых углов прямоугольного треугольника составляет 90°, то угол НКС=90-6=84°. Теперь рассмотрим полученный ∆ВСК. В нём: биссектриса делит прямой угол пополам, поэтому угол ВСК=90÷2=45°, угол СКВ=96°, и зная что сумма углов треугольника составляет 180°, то угол В=180-45-96=39°. Теперь найдём угол А. Угол А=90-39=51°