Утверждения 1) и 2) верные
Объяснение:
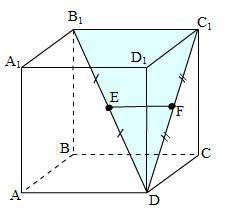
Смотри прикреплённый рисунок.
1) EF ║ B₁C₁ как средняя линия Δ DB₁C₁.
Если прямая (EF), не лежащая в плоскости (ABCD) параллельна прямой B₁C₁, лежащей в данной плоскости, то она параллельна этой плоскости. То есть EF ║ABCD или, что то же самое EF ║ABC, и утверждение 1) верное.
2) EF ║ B₁C₁ как средняя линия и B₁C₁ ║ А₁D₁ как параллельные рёбра куба. Следовательно, EF ║ А₁D₁.
Если прямая (EF), не лежащая в плоскости (AА₁D₁D) параллельна прямой A₁D₁, лежащей в данной плоскости, то она параллельна этой плоскости. То есть EF ║AА₁D₁D или, что то же самое EF ║AА₁D₁, и утверждение 2) верное.
3) EF ║ B₁C₁ как средняя линия и ребро куба B₁C₁ ⊥ плоскости грани АВВ₁А₁.
Если одна из параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости, то есть EF ⊥АВВ₁А₁ или, что то же самое EF ⊥ AА₁В₁, и утверждение 3) неверное.
4) Поскольку мы уже установили верные утверждения, то утверждение 4) неверное
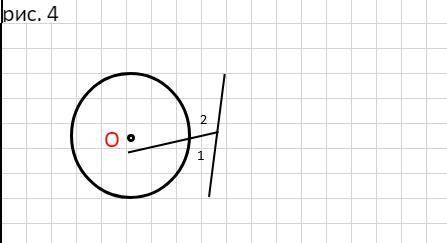
АВ - касательная;
АС -секущая;
СD - внутренний отрезок секущей (рисунок в приложении).
По условиям задачи:
АВ+АС=30 см
AB-CD=2
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть:
АВ²=АС*DA
Выразим:
AC=30-AB
CD=AB-2
Пусть АВ=х см, тогда
АС=30-х
СD=x-2
АС=DA-DC=30-x-x+2=32-2x
АВ²=АС*DA=(30-x)*(32-2x)
x²=(30-x)*(32-2x)
x²=960-32х-60х+2х²
2х²-х²-92х+960=0
х²-92х+960=0
D=b²-4ac=(-92)²-4*1*960=8464-3840=4624 (√4624=68)
x₁=(-b+√D)/2a=(-(-92)+68)/2*1=160/2=80 - не соответствует условиям задачи
x₂=(-b-√D)/2a=(-(-92)-68)/2*1=24/2=12
АВ=12 см
АС=30-АВ=30-12=18 см
ответ: касательная равна 12 см, секущая - 18 см.