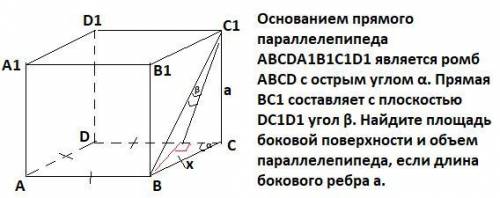
Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб АВСD с острым углом α. Прямая BC1 составляет с плоскостью DC1D1 угол β. Найдите площадь боковой поверхности и объем параллелепипеда, если длина бокового ребра а.
Объяснение:
S(бок)=Р*L, V=S(осн.)*L ,где L-боковое ребро , перпендикулярное плоскости основания.
Пусть сторона ромба х , ∠DCB=α , ВН⊥DC. Тогда углом между плоскостью (DC₁D₁) и прямой ВС₁ будет ∠ВНС₁=β .
ΔВНС-прямоугольный , ВН=х*sinα.
ΔBHC₁-прямоугольный , ВН=ВС₁*sinβ .
ΔBCC₁ прямоугольный ,BC₁=√(x²+a²), поэтому
ВН=√(x²+a²)*sinβ . Приравняем правые части для ВН и найдем сторону ромба.
х*sinα=√(x²+a²)*sinβ , х²*sin²α=(x²+a²)*sin²β , х²*sin²α-x²*sin²β=a²*sin²β , х²*(sin²α-sin²β)=a²*sin²β , х=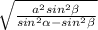
, x=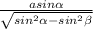
.
S(бок)=4а* 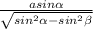, S(бок)=
.
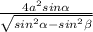V=а²sinα*а=а³sinα
==============
Угол между прямой и плоскостью .это угол между основанием перпендикуляра и основанием наклонной.
Прямая параллельна плоскости, если она параллельна какой-либо прямой из этой плоскости. Основание трапеции АД параллельно прямой MN, которая принадлежит плоскости α, следовательно АД || α. Доказано.
Как было уже сказано выше, средняя линия трапеции равна полусумме ее оснований, тогда
ВС + АД = 2 * MN = 2 * 8 = 16
ВС = 16 - 10 = 6
ответ: 6