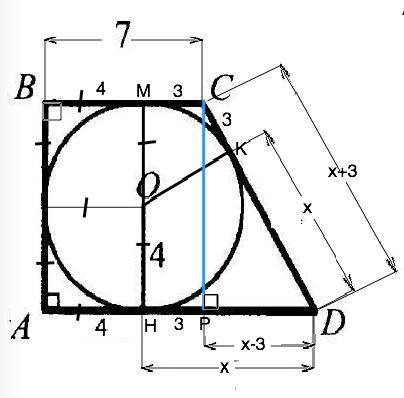
Вариант решения.
В прямоугольной трапеции АВСD радиус вписанной окружности 4, длина меньшего основания 7. Найдите площадь трапеции.
Высота трапеции равна диаметру вписанной окружности. АВ⊥АD ⇒ AB=h=2r=8.
Проведем радиусы ОМ к ВС и ОК к CD. Радиусы, проведенные в точку касания, перпендикулярны касательной. АВМН - прямоугольник. ВМ=АН=4. МС=7-4=3.
Отрезки касательных, проведенные из точки вне окружности, равны. СК=СМ=3 и НD=KD=х. Опустим высоту СР=AB=8. Отрезок НР=МС=3, PD=х-3, СD=х+3.
По т.Пифагора СD²-PD²=CP². (х+3)²-(х-3)² =64, откуда 12х=64 и х=5 1/3. Площадь трапеции равна произведению высоты на полусумму оснований. АD=AH+HD=4+5 1/3=9 ¹/₃. S(ABCD)=AB•(BC+AD):2=8•(7+9 ¹/₃):2. Ѕ(ABCD)=65 ¹/₃ ед. площади.
6) Хорды AB и CD пересекаются в точке E, тогда верно равенство
АE·BE=CE·DE
7) Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14) X Источник информации , r – радиус окружности, d – диаметр окружности.
8) Формула для вычисления площади круга
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415). 2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
9)Окружность называется вписанной в треугольник, если она касается всех его сторон. Окружность называется описанной около треугольника, если она проходит через все его вершины. Теорема 1. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.