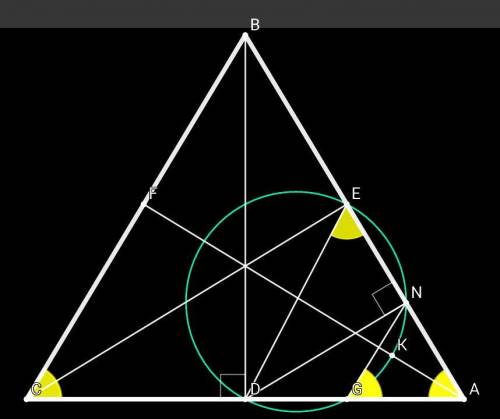
BD = 20, BE = 7, BC = 25, тогда из прям. ΔBEC и ΔBCD ⇒ CE = √(25² - 7²) = 24 ; CD = √(25² - 20²) = 15
Углы BEC и BDC видны из отрезка ВС под прямым углом ⇒ вокруг четырёхугольника BEDC можно описать окружность, т.е. сумма его противоположных углов в сумме дают 180°. Из этого следует, что ∠BCD = ∠AED, ∠CBE = ∠ADE ⇒ ΔАВС подобен ΔAED. Аналогично, четыр-ник ENCD - вписанный ⇒ ΔAED подобен ΔANG. Значит, ΔANG подобен ΔAED подобен ΔАВС, ∠АGN = ∠AED = ∠ACB, ∠ANG = ∠ADE = ∠ABC. Так как ∠ANG = ∠ABC, то NG || BC.
ΔABD подобен ΔАСЕ по двум углам ⇒ AD/AE = BD/СЕ = 20/24 = 5/6 ; Пусть AD = 5x, AE = 6x, тогда ΔAED подобен ΔАВС ⇒ AD/AE = AB/AC ; 5/6 = (6x + 15)/(5x + 7) ⇒ x = 3 . Значит, AD = 15, AE = 18. Заметим, что АВ = ВС = 25 ⇒ ΔАВС - равнобедренный, значит, ΔANG, ΔEAD - равноб-ые.
ΔАED - равноб-ый, DN - высота, медиана ⇒ AN = NE = 18/2 = 9
ΔABC - равноб-ый ⇒ CE = AF = 24 - по свойству высот, проведённых к боковым сторонам
ΔANG подобен ΔАВС: AN/AB = AK/AF ⇒ AK = (AN/AB)•AF = (9/25)•24 = 8,64
ответ: 8,64
Опустим высоты BH1 и CH2, BH1∩CH2=O, BH1=h1, CH2=h2. Тогда ∠AH1B=∠OH1C=∠CH2A=∠OH2B=90°.
Рассмотрим ΔAH2C. ∠H2СA=180°-90°-45°=45°=∠A(по условию)=> ΔAH2C равнобедренный => AH2=CH2=h2.
Рассмотрим ΔAH1B. ∠H1BA=180°-90°-45°=45°=∠A(по условию)=> ΔAH1B равнобедренный => AH1=BH1=h1.
Рассмотрим четырехугольник AH2OH1. ∠H2OH1=360°-90°-90°-45°=135°. => ∠BOH2=∠COH1=180°-135°=45°.
Рассмотрим ΔBH2O. ∠H2BO=180°-90°-45°=45°=∠BOH2(по доказанному ранее)=> ΔBH2O равнобедренный => BH2=OH2=a.
Рассмотрим ΔCH1O. ∠H1CO=180°-90°-45°=45°=∠COH1(по доказанному ранее)=> ΔCH1O равнобедренный => CH1=OH1=b.
BH1=h1=b+√(BH2²+OH2²)=a√2+b
CH2=h2=a+√(CH1²+OH1²)=a+b√2
Рассмотрим ΔBOC. По неравенству треугольника BC<BO+OC=√(BH2²+OH2²)+√(CH1²+OH1²)=a√2+b√2
Тогда P=AB+BC+AC=h2+a+h1+b+AC<h2+a+h1+b+a√2+b√2=h2+h1+(a+b√2)+(a√2+b)=h1+h2+h1+h2=2(h1+h2)
Ч.т.д.