5 номер
В равнобедренном треугольнике две стороны равны.
По неравенству сторон треугольника знаем, что сумма двух сторон треугольника не может быть меньше третьей.
Предположим, что третья сторона равна 4 см.
Проверим, 4+4<9 - не подходит.
9+9>4 - подходит, значит, третья сторона = 9 см
6 номер
1)Рассмотрим треугольник DME:
предположим ,что угол DME - тупой (будет смежным с острым углом этого треугольника) и
угол DEM - острый (так как двух углов тупых не может быть в треугольнике по определению и признаку треугольника) .
2)Если напротив большего угла в данном треугольнике лежит самая большая сторона,то DE>DM.
7 номер
<B = 180° - (79°+ 55°)= 46° .
<C = 180° - ( 46° + 55°) = 79° .
< А = 55° (по условию).
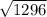 =36
=36
Проведём из вершины D высоту DА.
треугольник DАE - прямоугольный.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> DА = 16/2 = 8 см.
DА - и есть расстояние от точки D до прямой СЕ.
ответ: 8 см.
б)Проведём перпендикуляр от прямой с до вершины Е. (Пусть он будет назван НЕ)
треугольник СЕН - прямоугольный.
При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.
∠CED = ∠HCE = 30˚, как накрест лежащие.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> НЕ = 20/2 = 10 см.
НЕ - и есть расстояние от прямой с до прямой DE.
ответ: 10 см.