Обе задачи решаются однотипно.
Площадь сферы находят по формуле
S=4πR²
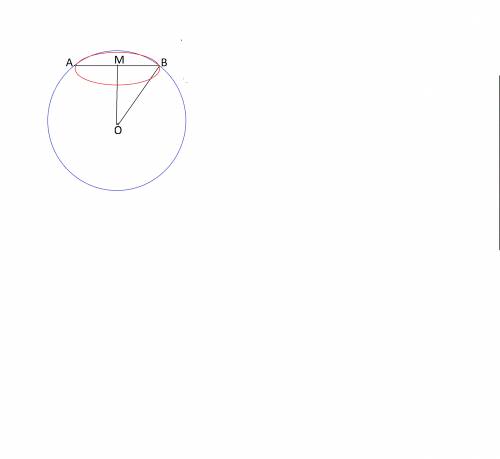
Для наглядности сделаем схематический рисунок осевого сечения шара, перпендикулярного данному сечению .
Сечение шара - круг. На рисунке он в разрезе выглядит линией.
АВ - его диаметр, а МВ- радиус.
ОМ - расстояние от центра круга до центра плоскости сечения, ОВ- радиус шара.
1) В шаре на расстоянии 12 см от центра проведено сечение
площадью 64 п
Найти площадь поверхности сферы.
Найдем квадрат радиуса сечения из его площади .
S=πr²
64π=πr²
r²=64
Из прямоугольного треугольника ОМВ по т.Пифагора найдем R² шара.
R²=64+144=208
S=4πR²=4*208π=832π
2)
Площадь сечения, удаленное от центра шара на 21 см, равна 784 п
Найти площадь поверхности сферы.
Найдем квадрат радиуса сечения из его площади .
784π=πr²
r²=784
R²=784+21²=441
S=4πR²=4π*441=1764π
------------------------
Если есть необходимость, можно вычислить площадь, умножив на π- в этом калькулятор.
Объяснение:
12
Если диагональ образует с площадью основания,то диагональ основания равна высоте прямоугольного параллелепипеда.
Найдём диагональ основания по теореме Пифагора:
h=d=13 см
S = 2(a · b + a · h + b · h)=2(12 · 5 + 12 · 13 + 5 · 13) =2(60+156+65) = =2*281=562 см²
V=a · b · h=12 · 5 · 13=780 см³
13
Если образующая конуса наклонена к плоскости основания на 45°,то радиус основания равен высоте.Примем радиус основания за х,тогда по теореме Пифагора:
l²=2r²
12²=2x²
x²=144:2
x²=72
x=√72=6√2 см
S=π r (r + l)=π6√2(6√2+12)=π72+π72√2=π72(1+√2) см²
V=144√2 π см³