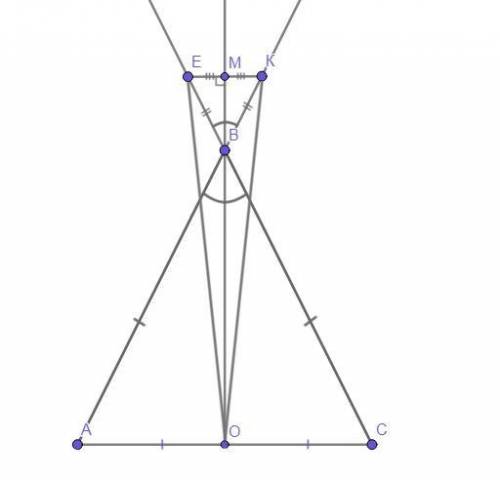
Чертёж смотрите во вложении.
Дано:
ΔАВС - равнобедренный (АС - основание).
Точка К ∈ лучу АВ.
Точка Е ∈ лучу СВ.
ВК = ЕВ.
О - середина АС.
Доказать:
ΔЕКО - равнобедренный.
Доказательство:
Рассмотрим ΔАВС - равнобедренный. Соединим вершину В и точку О. ВО - медиана, проведённая к основанию, а значит, также, биссектриса ∠АВС (по свойству равнобедренного треугольника).
∠АВС = ∠ЕВК как вертикальные, и если мы продлим биссектрису ВО до пересечения стороны ЕК в точке М, то она также будет биссектрисой ∠ЕВК (так как биссектрисы вертикальных углов лежат на одной прямой).
Рассмотрим ΔЕВК - равнобедренный (ВК = ЕВ по условию). ЕК - его основание, и к ней проведена биссектриса ВМ, а значит ВМ⊥ЕК и ЕМ = МК (ВМ - медиана и высота по свойству равнобедренного треугольника).
Рассмотрим весь ΔЕКО. Так как ОМ - медиана и высота одновременно, то ΔЕКО - равнобедренный (по признаку равнобедренного треугольника).
ответ: что требовалось доказать.
1) В
Объяснение:
1) Обозначим стороны треугольника, как х, у, z, когда для построения треугольника нужно, чтобы:
1.1) х<у+z
1.2) y<x+z
1.3) z<x+y
Как мы видим варианты А и С нам не подходят, значит правильный ответ- В
2) Прямые параллельны, если накрест лежащие углы равны, или если сумма односторонних углов равна 180°. Взяв 2-ую картинку мы видим, что сумма (односторонних) углов 149°+31°=180° (если я правильно понял чему равны углы), значит по теореме об односторонних углах, эти прямые параллельны
1)Так как АВ = ВС и ВК = ВЕ => ЕС = АК.
∠А = ∠С, по свойству равнобедренного треугольника.
2)Рассмотрим треугольники СЕО и АКО:
АК = ЕС, из 1)
АО = ОС, так как О - середина.
∠А = ∠С, из 1).
=> треугольники СЕО и АКО равны, по 1 признаку равенства треугольников.
=> ЕО = ОК.
А так как ЕО = ОК => треугольник ЕКО - равнобедренный.
Ч.Т.Д.