Question

В равностороннем треугольнике MNK проведена биссектриса KF, расстояние от точки F до прямой MK=8см. Найти расстояние от точки K до прямой MN. РЕБЯТА ОТ ТОГО КАК ВЫ ЕЁ РЕШИТЕ ЗАВИСИТ МОЯ ЧЕТВЕРТНАЯ ОЦЕНКА

Answer 1

Расстояние от точки K до прямой MN - отрезок FK, равный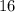 $16$ (см).

Объяснение:

1. Рассмотрим равносторонний ΔMNK:

Т.к. ΔMNK - равносторонний, то каждый угол будет равняться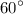 ${60}^{\circ}$.

По условию из точки K к отрезку MN проведём биссектрису KF, которая по свойству делит ∠K на два равных угла.

⇒ ∠NKF = ∠FKM = 60° : 2 = 30°.

Расстояние от точки до прямой/отрезка - перпендикуляр.

⇒ Проводим из вершины F перпендикуляр к отрезку MK, равный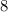 $8$ (см).

Благодаря этому перпендикуляру, получаем прямоугольный ΔFGK с прямым углом G (оставшиеся два угла - острые).

2. Рассмотрим прямоугольный ΔFGK:

Катет, лежащий напротив угла в 30°, равен половине гипотенузы.

⇒ катет FG в 2 раза меньше гипотенузы FK, т.е. FK =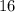 $16$ (см).

Т.к. ΔMNK - равносторонний ⇒ он является и равнобедренным с основанием NM.

Биссектриса, проведённая к основанию равнобедренного треугольника, является и высотой, и медианой.

⇒ биссектриса FK - высота треугольника MNK, и в тоже время перпендикуляр к прямой MN.

⇒ отрезок FK - расстояние от точки K до прямой MN.