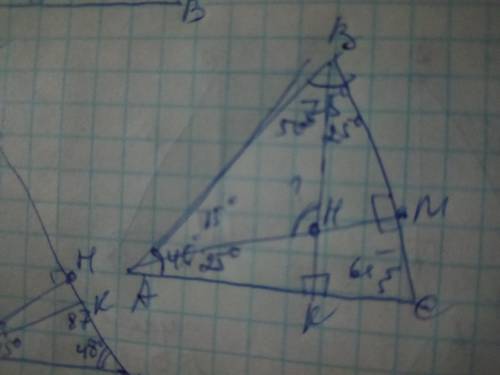
Зная, что ∠ВАС=40°, а угол АВС=75°, и сумма углов треугольника составляет 180°, найдём угол С.
Угол С=180-40-75=65°. Рассмотрим полученный ∆САМ. Он прямоугольный так как УГОЛ АМС=90°, найден угол С=65°, и так как сумма острых углов прямоугольного треугольника составляет 80°, то угол САМ=90-65=25°. Если угол САМ=25°, то угол ВАН=40-25=15°. Рассмотрим ∆СВК. Он также прямоугольный, так как угол ВКС=90°, угол С=65°, поэтому угол СВК=90-65=25°. Если угол СВК=25°, то угол АВН=75-25=50°
Теперь рассмотрим ∆АВН. В нём известны 2 угла: угол ВАН=15°, а угол АВН=50° и можно найти АНВ. Угол АНВ=180-50-15=115°
ОТВЕТ: угол АНВ=115°
Котангенс - это отношение прилежащего к углу катета к противолежащему, хотя в данной задаче на этом можно и не сосредотачиваться. В прямоугольном треугольнике два другие угла всегда острые. Значит Проводим прямую и строим перпендикуляр к ней. О-точка их пересечения.
1) От точки О на одной прямой откладываем какой-либо отрезок и ставим точку А, а на другой откладываем два таких отрезка и ставим точку В. Получим ctgА=1/2.
2) 1,5=3/2. То же самое, но теперь откладываем на прямых три отрезка и два отрезка, т.е. АО=3, ВО=2.
3) 0,8=8/10=4/5. То же, только АО уже будет 4 отрезка, ВО - 5 отрезков.