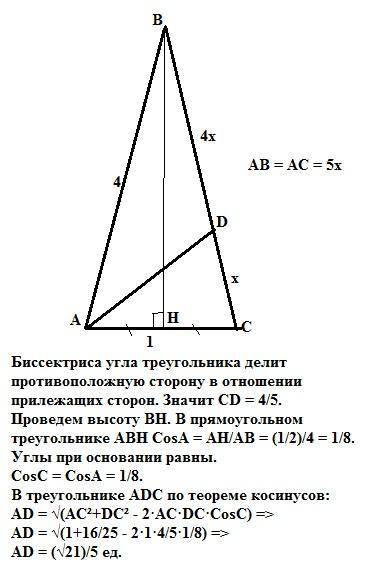
AD = (√21)/5 ед.
Объяснение:
Биссектриса AD угла А треугольника АВС делит противоположную сторонуВС в отношении прилежащих сторон.
То есть BD/DC = 4/1. ВС =АВ = 4 ед.
Значит СD = 4/5 ед.
Проведем высоту ВН. В равнобедренном треугольнике АВС высота является и медианой. АН = НС = 1/2 ед.
В прямоугольном треугольнике АВН
CosA = AH/AB = (1/2)/4 = 1/8.
Углы при основании равнобедренного треугольника равны.
CosC = CosA = 1/8.
В треугольнике ADC по теореме косинусов:
AD = √(AC²+DC² - 2·AC·DC·CosC) =>
AD = √(1+16/25 - 2·1·4/5·1/8) => AD = √(21/25).
AD = (√21)/5 ед.
Дано:
АВСА1В1С1 - прямая призма
АВ = 3 см
АС = 8 см
АА1 = 15 см - высота призмы
Найти:
S(бок) , S(полн) , V.
Решение.
Запишем уравнение теоремы косинусов
a^2 = b^2 + c^2 + 2bc*cos(a)
Рассмотри треушольник АВС. По теореме косинусов имеем
ВС^2 = AC^2 + AB^2 - 2*AC*AB*cos(60) =
= 8^2 + 3^2 - 2*8*3*0,5 =
= 64 + 9 - 24 =
= 49
тогда ВС = 7 см
Площадь боковой поверхности S(бок) прямой призмы
S(бок) = АА1*(АВ + АС + ВС) =
= 15(3 + 8 + 7) =
= 270 см^2
Найдем площадь основания S(осн) как площадь треугольника по двум сторонам и синус угла между ними
S(осн) = 0,5*АВ*АС*sin(60) =
= 0.5*3*8*кор (3)/2 =
= 6*кор (3) см^2
Полщадь полной поверхности S(полн) прямой призмы
S(полн) = S(бок) + S(осн) =
= 270 + 6*кор (3) см^2
Объем V прямой призмы
V = S(осн) *h =
= 6*кор (3)*15 =
= 90*кор (3) см^3
ответ: S(бок) = 270 см^2, S(полн) = 270 + 6*кор (3) см^2, V = 90*кор (3) см^3.