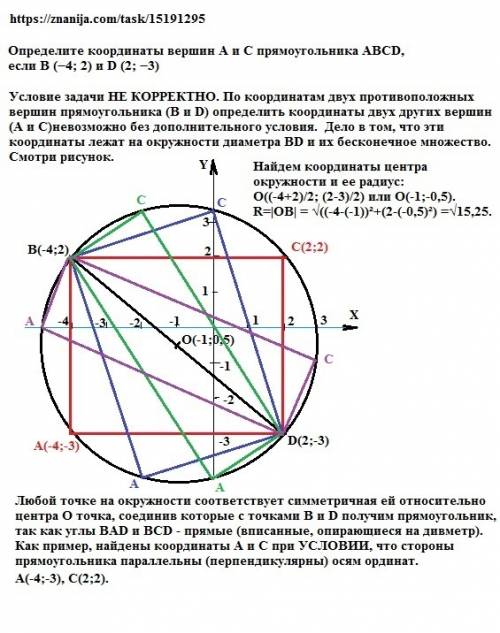
Условие задачи НЕ КОРРЕКТНО. По координатам двух противоположных вершин прямоугольника (B и D) определить координаты двух других вершин (А и С) невозможно без дополнительного условия. Дело в том, что вершины прямоугольника лежат на окружности диаметра BD и их бесконечное множество.
Смотри рисунок.
Любой точке на окружности соответствует симметричная ей относительно центра О точка, соединив которые с точками В и D получим прямоугольник, так как углы ВАD и ВСD - прямые (вписанные, опирающиеся на дивметр).
Найдем координаты центра окружности, описанной около данного прямоугольника и ее радиус:
О((-4+2)/2; (2-3)/2) или О(-1;-0,5).
R=|ОВ| = √((-4-(-1))²+(2-(-0,5)²) =√15,25. Тогда уравнение окружности (x+1)² + (y+0,5)² =15,25.
ЛЮБАЯ точка на этой окружности - вершина А, симметричная ей относительно центра О точка - вершина С.
Найдем координаты вершин А и С ПРИ УСЛОВИИ, что стороны прямоугольника параллельны осям ординат.
В уравнение окружности подставим координату Х=-4 и найдем для нее соответствующую координату Y: (-3)² + (y+0,5)² =15,25. => Y² + Y -6 = 0. => Y1=3, Y2=-2. Точно так же для точек с координатой Х=2. Y1=2 и Y2=-3. Тогда имеем: А(-4;-3) и С(2;2).
1) Пусть АВСD - трапеция, Вс-4 дм, AD-25 дм, АВ-20 дм, CD313 дм. Площадь трапеции можно найти по формуле: S-12(BC+AD)'h. 2) Опустим высоты һ%3DВЕ-CF. ДАЕВ и ДDFC -прямоугольные. Обозначим АЕ-х, тогда FD-25-(x+4)-21-х. Из ДАЕВ по т.Пифагора находим высоту h*-ВЕ?-AВ-АЕ?-202-x?. Из ДDFC по т.Пифагора находим высоту h?-CF2-CD-FD?-132-(21-х)2. Так как высоты равные, приравниваем полученные выражения и решаем уравнение: 202x-137-(21-х)3; 400-x-169-441+42х-x?3; 42х-672; X-16. Находим высоту трапеции: h-V(202-16?)-V(400-256)-v144-12 (дм). 3) S-1/2(BC+AD)"'h-1/2(4+25)"12-6'29-174 (дм?). ответ: 174 дм?.