
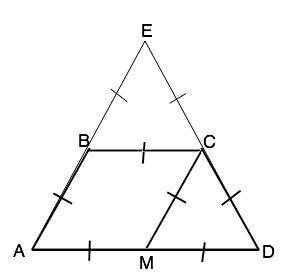
В трапеции АВСD стороны AB=BC=CD, следовательно, трапеция АВСD- равнобедренная.
Проведем СМ параллельно АВ. Противоположные стороны четырехугольника АВСМ параллельны. ABCD – параллелограмм. ⇒ СМ=АВ=СD. Т.к. АD=2 ВС, CМ=МD и СМ=СD. Поэтому треугольник СМD- равносторонний, ⇒ ∠СDM=60°. По свойству внутренних односторонних углов при параллельных ВС||AD и секущей СD ∠ВСD=180°-60°=120°. В равнобедренной трапеции углы при боковых сторонах равны. ⇒ ∠А=∠D=60°, ∠B=∠C=120°
–––––––––––––
Вариант решения: можно продолжить боковые стороны трапеции до их пересечения в точке Е. Тогда ВС - средняя линия ∆ АЕD, и АЕ=DE=AD. ∆ AED - равносторонний, ⇒ ∠A=∠D=60°, а ∠B=∠C=120°
Опуская перпендикуляры из Н к катетам основания-получаю НН1 и НН2.
С высотой пирамиды НS они образуют прямоугольные треугольники.
В этих треугольниках SH-общая высота и одинаковый угол бетта по условию.
Учитывая что высота в них может быть выражена SH=HH1*tgβ=HH2tgβ-следует
что НН1=НН2.
Теперь надо выразить это НН1 через а и ∠α. Н делит гипотенузу на две части b и a-b, выражу b через а...-второй рисунок
Высота пирамиды HS=HH1*tg β=a*sinα*cosα*tgβ/(sinα+cosα)
Площадь основания S(осн)=a^2*sinα*cosα/2
Тогда объем пирамиды V=S(осн)*SH/3=a^3*sin^2(2α)*tgβ/(24(sinα+cosα))