В треугольнике ABC провели ED∥CA.
Известно, что:
D∈AB,E∈BC, AB= 10 см, DB= 2 см, CA= 13 см. Вычисли ED.
Сначала докажи подобие треугольников. (В каждое окошечко пиши одну большую латинскую букву.)
∢BDE=∢B __ C,т.к. соответственные углы∢B
D=∢B __ CA,т.к. соответственные углы}⇒ΔAB __
∼ΔDB __ ,
ED= __ см.
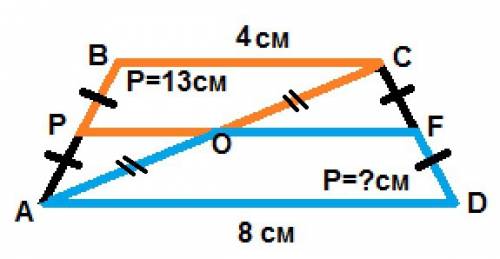
условие про биссектрису означает, что диагонали в точке пересечения делятся в отношении 8/6, но это означает, что основания трапеции отностятся как 8/6, то есть малое основание равно 6 (ясно, что треугольники, образованные основаниями и диагоналями, подобны).
Осталось найти высоту трапеции. К сожалению, подбор чисел подкачал. Из прямоугольного треугольника находим одну из диагоналей,
d1 = корень(8^2 - 6^2) = 2*корень(7);
d1*6 = h*8 (это просто удвоенная площадь прямоугольного треугольника), то есть
h = 3*корень(7)/2;
S = (3*корень(7)/2)*(8 + 6)/2 = 21*корень(7)/2