Sпол = 64(1+√3) см²
Объяснение:
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.Sполн. = Sбок. + Sосн.
Так как основанием правильной четырёхугольной пирамиды является квадрат, то площадь основания вычисляется по формуле:
Sосн = а², а - сторона квадрата
Формула площади боковой поверхности правильной пирамиды (Sбок):
Sбок = 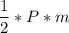 ,
,
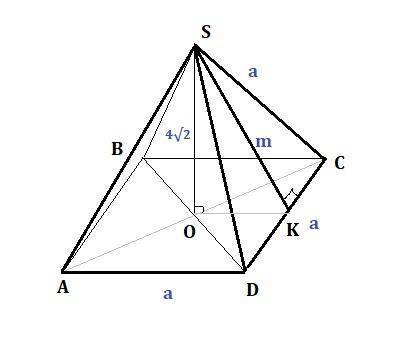
где Р - периметр основания, Р=4а, m-апофема (опущенный перпендикуляр SK из вершины S, на ребро основания DC)
Так как боковые грани – правильные треугольники, то высота SK является так же медианой: КС= DC/2 = а/2. Стороны SC=DC=SD=a.
∠SCD=∠SDC=∠DSC=60°.
Рассмотрим прямоугольный треугольник SKC.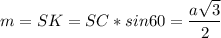
SO⊥(ABC) ⇒ SO⊥OK - как высота пирамиды, SK⊥DC - апофема, ⇒OK⊥DC (по теореме о трёх ⊥). ОК= а/2
2. Рассмотрим прямоугольный треугольник SOK.
По теореме Пифагора:
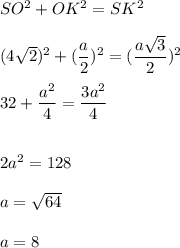
3. Sполн. = а² + 2*a*m =
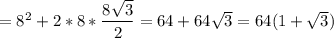
Дано : ΔABC, ∠C = 90°, CN = 1 см, NB = 2 см,
вписанная окружность (O; r)
Найти : S, r, R
Так как окружность вписана в треугольник, то стороны треугольника являются касательными к окружности. Радиус, проведённый в точку касания, перпендикулярен касательной в этой точке.
ON⊥CB, OK⊥AC, OM⊥AB
⇒ CKON - квадрат со стороной, равной радиусу вписанной окружности
⇒ r = CK = KO = JN = CN = 1 см
Отрезки касательных к окружности, проведённые из одной точки, равны
BM = BN = 2 см; AK = AM = x см
ΔABC :
BC = CN + BN = 1 см + 2 см = 3 см
AC = AK + KC = (x + 1) см
AB = AM + MB = (x + 2) см
Площадь прямоугольного треугольника можно вычислить через полупроизведение катетов или через произведение полупериметра на радиус вписанной окружности.
AC = x + 1 = 4 см; AB = x + 2 = 5 см
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы
ответ : S = 6 см², r = 1 см, R = 2,5 см