ответ: Объем шарового сегмента опущенного в цилиндр = π*468 см³
Объяснение: Дано:
Диаметр шара = 30 см тогда его радиус R = 15
Радиус основания цилиндра r = 12см
Найти объем шарового сегмента, опушенного в цилиндр V - ?
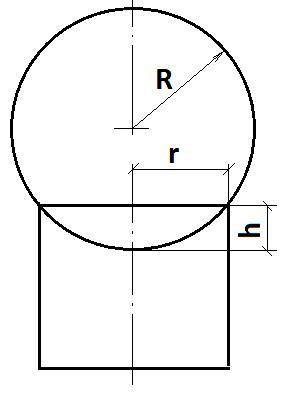
Смотрите рисунок. Что бы найти объем надо найти размер h - глубину погружения шара. По теореме Пифагора R² = r² + (R-h)² Получили квадратное уравнение: h² - 2Rh + r² = 0
h1,2 = (2R+-√4R² - 4r²)/2 = (2R+-2√R²-r²)/2 h = 6 см
Объем шарового сегмента найдем по формуле V = π*h²(R - h/3) = π*468 см³
Рассмотрим все случаи, с учетом неравенства треугольников. т.е. всякая стороны должна быть меньше суммы двух других сторон . Тогда можно построить треугольник. Из четырех чисел выбрать три существует всего неравенство нарушается, т.к. 2=3=5, и все вершины лежат на одной прямой. Нельзя построить.
2) 2;3;4, проверяем 3 меньше 2+4, 2 меньше 3+4, 4 меньше 2+3 Можно построить треугольник.
3)3;4;5 проверяем 3 меньше 4+5, 4 меньше 3+5, 5 меньше 3+4 треугольник можно построить.
4)2;4;5 т.к. 2 меньше 4+5, 4 меньше 2+5, 5 меньше 2+6, то такое треугольник можно построить.
ответ три
ответ: sqr (66)
Объяснение:
найди координаты вектора -2а
=(-4; -10 ; 8) и координаты вектора 3b =(-3; 6; -9)
найди координаты суммарного вектора (-7; -4; -1)
Теперь найди длину ( модуль) полученного вектора =
sqr( 49+16+1)=sqr(66)