1) Через середину гипотенузы строим прямую а, перпендикулярную основанию.
2) В плоскости, которая задается этой прямой и ребром AD проводим серединный перпендикуляр к AD.
3) Точка пересечения серединного перпендикуляра и прямой а - центр описанной сферы.
Объяснение:
Если сфера описана около данной пирамиды, то основание пирамиды вписано в окружность - сечение сферы.
Основание - прямоугольный треугольник. Центр описанной около него окружности лежит на середине гипотенузы.
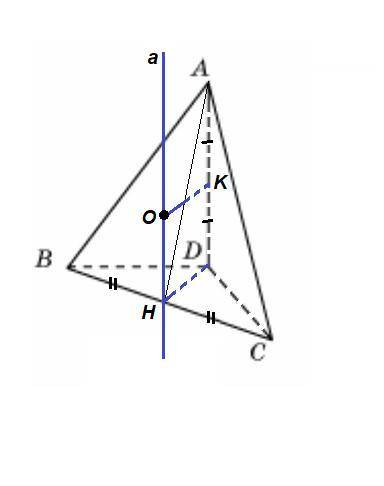
Пусть Н - середина гипотенузы ВС прямоугольного треугольника BCD.
Тогда точка Н - центр окружности, описанной около ΔBCD, равноудалена от всех вершин основания.
Отрезок, соединяющий центр сечения сферы с центром сферы, перпендикулярен сечению.Проведем через точку Н прямую а║AD. AD⊥(BCD), так как AD⊥BD и AD⊥DC, значит а⊥(BCD).
Центр сферы будет лежать на прямой а.
Любая точка прямой а равноудалена от вершин основания. Осталось найти на ней точку, удаленную от вершины А на то же расстояние, что и от остальных вершин.
Для этого в плоскости (ADH) проведем серединный перпендикуляр к ребру AD. К - середина AD, проведем КО║DН до пересечения с прямой а.
О - центр сферы.
1) <C = 180° - 100° = 80°.
2) <A = 180° - 40° - 80° = 60°
ответ: <A = 60°.
Рис.21) <A = 180° - 150° = 30°
2) <C = 180° - 90° = 90°
3) <B = 180° - 30° - 90° = 60°
ответ: <A = 30°, <B = 60°
Рис.31) <B = 40° , т.к. углы вертикальные
2) <C = 180° - 120° = 60°
3) <A = 180° - 40° - 60° = 80°.
ответ: <A = 80°, <B = 40°
Рис.41) <B = 180° - 140° = 40°
2) <A = <C = (180-40):2 = 70°, т.к. тр. ABC равнобедренный, а в нем углы при основании равны.
ответ: <A = <C = 70°
4/3
Объяснение:
Сначала найдем площадь фигуры, составленной из 1 и 2.
Площадь прямоугольного треугольника находится по формуле:
(катет)*(катет) / 2 = 4*2/2 = 4
Теперь найдем площадь фигуры 1.
Она равна ∫ от 0 до 2 x^2 dx.
Для того, чтобы вычислить определенный интеграл, нужно:
1) найти первообразную функции. Она равна x^3/3 + C.
2) воспользоваться формулой Ньютона-Лейбница:
2^3/3 - 0^3/3 = 8/3
Площадь фигуры 2 равна 4 - 8/3 = 12/3 - 8/3 = 4/3