Question

Дан треугольник АВС, ∠С=〖90〗^0,АС=3√3,ВС=3.

Найдите:
а) меры углов треугольника АВС;
б) радиус окружности, описанной вокруг треугольника АВС;
в) длину окружности, вписанной в треугольник АВС;
г) площадь сегмента в описанном вокруг треугольника АВС круге, который ограничен хордой АС и не содержит точки В.
Желательно все

Answer 1

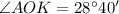
Объяснение:

Найдем гипотенузу АВ по Пифагору:

AB^2 = AC^2+BC^2 = 27+9= 36, отсюда гипотенуза АВ = 6

У описанной окружности, диаметром будет гипотенуза. Значит

радиус описанной окружности R=3

Радиус вписанной окружности r = (a+b-c)/2 = 1,5($\sqrt{3}$+1)-3 (a  и b катеты, с - гипотенуза)

Против угла А лежит катет ВС, равный половине гипотенузы.

Значит <A = 30°  а <B = 90°-30° = 60°

Сектор, содержащий хорду АС имеет угловую величину центрального угла АОС = 2-<B = 2*60 = 120°, значит площадь сектора в 3 раза меньше площади круга

S=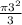$\frac{\pi 3^2}{3}$ = 3π Отнимем отсюда площадь треугольника АОС и получим площадь сегмента

S(AOC) = 0,5S(ABC)=0,5*0,5*AC*BC = 0,25*3$\sqrt{3}$*3 = 2,25$\sqrt{3}$

S(сег) = S - S(АОС) = 3π - 2,25$\sqrt{3}$ = $\sqrt{3}$($\sqrt{3}$π-2,25)