Выразим у в уравнении прямой:
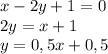
Параллельные линии имеют одинаковые коэффициенты перед иксом, поэтому запишем в общем случае уравнение такой касательной:
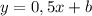
Суть касательных в том, что бы они имели 1 общую точку с графиком. Такие точки в нашем случае можно найти, если уравнение эллипса и уравнение касательной решить в системе, и при этом потребовать, что бы система имела ровно одно решение.
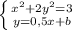
Подставим в первом уравнении вместо игрека второе уравнение, и теперь будем рассматривать отдельно только первое уравнение.
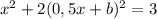
Здесь b идёт в качестве параметра. Для каждого решения этого уравнения (игрека) по второму уравнению можно найти икс (хотя здесь этого делать не нужно). Отсюда важный вывод - система имеет столько же решений, сколько это уравнение.
Найдём те значения параметра, при которых это уравнение будет иметь ровно одно решение.
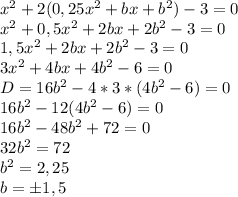
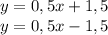
Розглянемо трикутники АВМ і А1В1М1. За умовою АВ = А1В1, АМ = А1М1, ﮮВАС = ﮮВ1А1С1. Оскільки АМ і А1М1 – бісектриси рівних кутів ВАС і В1А1С1, тоді ﮮВАС = 2ﮮВАМ = ﮮВ1А1С1 = 2ﮮВ1А1М1, тобто ﮮВАМ = ﮮВ1А1М1. За двома сторонами та кутом між ними ∆ВАМ = ∆В1А1М1. У рівних трикутників відповідні сторони та кути рівні АВ = А1В1, ﮮВМА = ﮮВ1М1А1. Розглянемо трикутники АМС і А1М1С1. За умовою ﮮВАС = 2ﮮМАС = ﮮВ1А1С1 = 2ﮮМ1А1С1, тобто ﮮМАС = ﮮМ1А1С1, переконаємось, що ﮮАМС = ﮮА1М1С1, тобто різниця величин двох кутів дорівнює нулю. Кути розгорнуті ﮮВАС = ﮮВ1М1С1 = 180˚. Тому ﮮАМС – ﮮА1М1С1 = (180˚ - ﮮВМА) – (180˚ - ﮮВ1М1А1) = ﮮВ1М1А1 – ﮮВМА = 0˚. За стороною і двома прилеглими кутами ∆АМС = ∆А1М1С1. У рівних трикутників відповідні сторони і кути рівні АС = А1С1, ﮮАСВ = ﮮА1С1В1, МС = МС1. За основною властивістю довжини відрізка ВС = ВМ + МВ = В1С1 = В1М1 + М1С1. Трикутники АВС і А1В1С1 рівні.