Question

Решить ! две окружности, радиусы которых равны r и 3r, касаются внешне в точке k. к этим окружностям провели общую внешнюю касательную mn (точка m принадлежит большей окружности, точка n — меньшей).1) докажите, что центры этих окружностей и точка их касания k лежат на одной прямой.2) вычислите площадь фигуры kmn, ограниченной меньшими дугами ∪km и ∪kn этих окружностей и отрезком mn.

Answer 1

1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.

2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.

Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора $AD=\sqrt{AB^2-BD^2}=2\sqrt3r$.

Площадь трапеции ANMB равна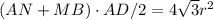 $(AN + MB) \cdot AD / 2 = 4\sqrt3r^2$

Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна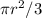 $\pi r^2/3$

Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна $\pi(3r)^2/6=3\pi r^2/2$

Площадь искомой фигуры

$4\sqrt3r^2-\dfrac{\pi r^2}{3}-\dfrac{3\pi r^2}2=\left(4\sqrt3-\dfrac{11\pi}6\right)r^2$