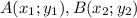
Координаты середины отрезка
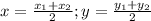
Расстояние между точками
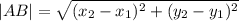
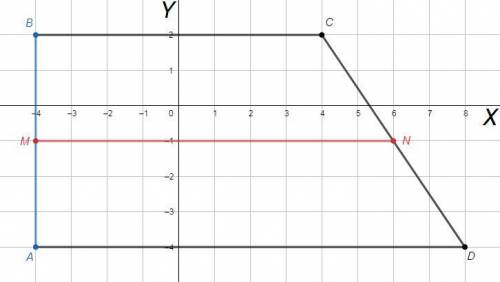
А(-4;-4), B(-4;2), C(4;2), D(8;-4)
MN - средняя линия трапеции.
M - середина AB
M( (-4+(-4))/2 ; (-4+2)/2 ) = M(-4;-1)
N - середина CD
N( (4+8)/2 ; (2+(-4))/2 ) = N(6;-1)
|MN|= √( (6-(-4))^2 + (-1-(-1))^2 ) =√(100+0) =10
Точки A и D имеют равные координаты по оси Y => AD||X'X (отрезок AD параллелен оси X)
Аналогично BC.
Основания параллельны оси X.
Точки A и B имеют равные координаты по оси X => AB⊥X'X (отрезок AB перпендикулярен оси X)
AB - высота трапеции.
|AB|= √( (-4-(-4))^2 + (2-(-4))^2 ) =√(0+36) =6
S(ABCD) =MN*AB =10*6 =60
Щоб побудувати точку C', у яку перейде точка C внаслідок повороту навколо точки O на кут α=90 градусів, потрібно (дивись рисунок):
а) провести промінь OC;
б) від променя OC відкласти кут COK, що дорівнює куту α у заданому напрямку (за умовою цього завдання – проти годинникової стрілки на кут α=90);
в) на промені OK знайти точку C', яка лежить на відстані OC від центру повороту O. Знайдемо довжини відрізка OC (і відповідно OC'):
Якщо на промені OK від точки O відкласти відрізок |OC'|= √10, то отримаємо координати точки C'(-3;1).
Звичайно, що точно відкласти довжини більшості відрізків не зручно (або неможливо), тому для пошуку координат точки (x';y'), при попороті точки (x;y) на кут α проти годинникової стрілки, зручно використовувати формули:
у нашому випадку, отримаємо
Відповідь: (-3;1) – А.
Объяснение: