Найти площадь равнобедренного треугольника высота которого приведённая к основанию равна 10 см а боковая сторона 26 см

👇

Увидеть ответ

Ответ:

kosonogova

10.07.2021

Высота делит равнобедренный треугольник на два прямоугольных треугольника:

Гипотенуза у них равна ребру треугольника и равна 26 см (из условия)

Один из катетов у них общий и равен высоте (10 см)

Найдем у первого треугольника неизвестный катет, являющийся половиной от основания:

Для этого используем Обратную Теорему Пифагора:

$\sqrt{676-100} =\sqrt{576} = 24$

Катет соответств. половине основания равен 24 см.

Тогда полное основание равно двум таким катетам(т.к треугольники одинаковые) = 24+24=48 см.

Теперь уже воспользуемся формулой Герона:

$\sqrt{50(50-26)(50-26)(50-48)}=\sqrt{50*24*24*2} =24\sqrt{100} =24*10=240$

Площадь равнобедренного треугольника равна 240 см^2

4,5(76 оценок)

Открыть все ответы

Ответ:

aika043

10.07.2021

1)Два треугольника называются подобными, если их углы соответственно равны

1) да ; 2) нет

Вспомним 1-й признак подобия:

если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

2)Любые два прямоугольных и равнобедренных треугольника подобны.

1) нет ;2) да

Верно. По первому признаку. Углы при основании равны 45°,а напротив основания 90°

3)Любые два прямоугольных треугольника подобны.

1) да 2) нет

В таких треугольниках мы можем утверждать только о равенстве одного угла-прямого. Ни для одного признака подобия этого недостаточно

Неверно

4 )Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны

1) да 2) нет

Более подходящие признаки

2-й -если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны. Равенство углов нам не дано. Утверждать не можем

3-й -: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны. Нам даны по 2 стороны. Утверждать не можем

5)Если два треугольника подобны, то их соответствующие стороны равны

1) да; 2) нет

3-й признак: если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.

6)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

1) да ; 2) нет

Теорема верная.

7)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

1) да ; 2) нет

Это первый признак равенства. А,равные треугольники подобны

8)Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.

1) да ; 2) нет

Вспомним 1-й признак подобия:

4,7(90 оценок)

Ответ:

karen781

10.07.2021

ответ:

Всё в разделе "Объяснение".

Объяснение:

1. Неверно.

Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

2. Верно.

Это 2 признак подобия треугольников.

3. Верно.

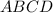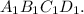
Даны два квадрата. Назовём их ABCD и A_1B_1C_1D_1.

Проведём диагональ 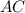в квадрате 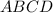ABCD и диагональ 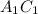A_1C_1 в квадрате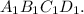 A_1B_1C_1D_1.

Рассмотрим 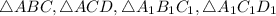$\triangle ABC, \triangle ACD, \triangle A_1B_1C_1, \triangle A_1C_1D_1$ .

У квадрата все углы прямые.

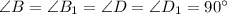$\angle B = \angle B_1 = \angle D = \angle D_1 = 90^{\circ}$ , по свойству квадрата.

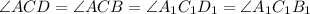$\angle ACD = \angle ACB = \angle A_1C_1D_1 = \angle A_1C_1B_1$ , так как диагонали квадрата делят углы пополам.

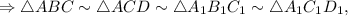$\Rightarrow \triangle ABC\sim \triangle ACD \sim \triangle A_1B_1C_1 \sim \triangle A_1C_1D_1,$ по 1 признаку подобия треугольников.

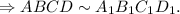
$\Rightarrow ABCD\sim A_1B_1C_1D_1.$

4. Неверно.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.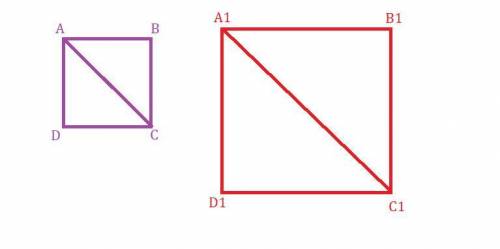
15 . заранее . подобные треугольники установите, истинны или ложны следующие высказывания: 1. два тр