30 градусов
Объяснение:
Если наклонная 5, а ее проекция 3, то оставшаяся сторона этого незамысловатого треугольника равна 4 (Египетский треугольник), то для треугольника с гипотенузой-наклонной 8 этот полученный катет тоже является катетом, противолежащим нужному углу. Катет, противолежащий угол и гипотенузв связаны через синус угла.
синус этого угла равен 4:8=1/2, а значит сам угол равен 30 градусов
Раз Вы еще не проходили решение задач с синусов, вот дополнение к первому решению.
Вы уже поняли, как найдены стороны параллелограмма.
Периметр его 40. Если принять меньшую сторону за х, то большая сторона будет х+2
Запишем
2(х+х+2)=40
4х=36
х=9 -это меньшая сторона.
9+2=11- это большая сторона.
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°
Приняв один из углов за у, запишем:
у+ у+120=180°
2у=60°
у=30°
Нашли, что острый угол параллелограмма равен 30°
Сделайте простейший рисунок.
Опустите из вершины тупого угла на любую сторону высоту.
Пусть это будет высота ВН на сторону АD
ВН противолежит углу 30°
Вы уже учили, что катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы.
У нас прямоугольный треугольник АВН, угол ВАН=30°
Следовательно, высота параллелограмма равна половине АВ и длина ее зависит от того, к какой стороне она проведена.
1) ВН=11:2=5,5 см
Площадь параллелограмма равна произведению высоты на сторону, к которой она проведена:
S=5,5*9=49,5 cм²
или
2)ВН=9:2=4,5 см
и тогда
S=4,5*11=49,5 см²
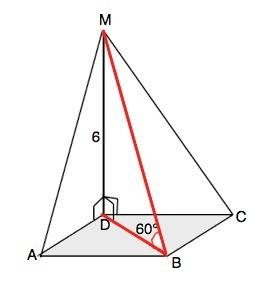
а) По условию MD перпендикулярна плоскости квадрата,
АD -проекция АМ на плоскость квадрата.
СD - проекция СМ на плоскость квадрата.
По т. о 3-х перпендикулярах МА⊥АВ, и МС⊥СВ.
Углы МАВ и МСВ прямые,⇒ ∆ МАВ и Δ МСВ прямоугольные.
б) В прямоугольном ∆ МDB катет DB равен MD:tg60°=6:√3=2√3
BD- гипотенуза прямоугольного равнобедренного ∆ ABD, его острые углы=45°.
АВ=ВD•sin45°=2√3•√2/2=√6
в) МD перпендикулярна плоскости квадрата по условию.
В ∆ АВD катет АD является проекцией наклонной АМ на плоскость квадрата.
Гипотенуза DB является проекцией МВ на плоскость квадрата.
АВ - общий катет ∆ АМВ и ΔΔ ADB. ⇒ ∆ ABD является проекцией ∆ MAB на плоскость квадрата.
в) В ∆ МАВ по т. о 3-х перпендикулярах наклонная МА⊥АВ,⇒
∆ МАВ прямоугольный.
Ѕ=AM•AB:2
Из ∆ АМD по т.Пифагора АМ=√(MD²²+AD²²)=√(36+6)=√42
S=√42•√6=√(7•6•6)=6√7 см²
ответ: 30°
Объяснение: