1.∠A=∠C= (180°-80°)/2 =50°
2.∠ABM=∠CBM=80°/2=40°
3.∠AMB=∠CMB=90°
Объяснение:
1. По свойству равнобедренного треугольника углы при основании равны. Зная что сумма углов треугольника =180 получаем 80+2х=180, откуда х=50° т.е. ∠BAM=∠BCM= (180°-80°)/2 =50°
2. Рассмотрим получившиеся треугольники AMB и CMB:
AB=BC(условие), AM=MC(BM-медиана), ∠BAM=∠BCM
следовательно ΔAMB = ΔCMB(1-й признак равенства треугольников).
3. ∠ABM=∠CBM=80°/2=40°
∠AMB=∠CMB=180°/2=90°
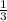 BK=
BK= . Значит, DK=2NK=2
. Значит, DK=2NK=2 . Считаем площадь равнобедренного ADC=
. Считаем площадь равнобедренного ADC=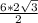 =6
=6 . Получаем, наконец, площадь полной поверхности: 3
. Получаем, наконец, площадь полной поверхности: 3 +3*6
+3*6 =21
=21 (площадь основания плюс площади трех боковых граней).
(площадь основания плюс площади трех боковых граней). . И наконец, V=9
. И наконец, V=9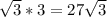
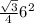 =9
=9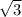 . Идем дальше. Чтобы найти площадь боковой грани ADC (хотя все три равны) надо найти высоту треугольника ADC - DK. Для этого рассм. треуг. DNK. В нем угол DKN=60. Значит, KDN=180-90-60=30. Т.е. в нем DK=2NK (катет, противолежащий углу 30 гр., равен половине гипотенузы). Где возьмем NK? Из равностороннего ABC, где BK - медиана и высота, а значит ВК=
. Идем дальше. Чтобы найти площадь боковой грани ADC (хотя все три равны) надо найти высоту треугольника ADC - DK. Для этого рассм. треуг. DNK. В нем угол DKN=60. Значит, KDN=180-90-60=30. Т.е. в нем DK=2NK (катет, противолежащий углу 30 гр., равен половине гипотенузы). Где возьмем NK? Из равностороннего ABC, где BK - медиана и высота, а значит ВК=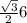 =3
=3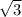 . А NK=
. А NK=
равнобедренный △АВС.
АВ = ВС
∠В = 80°
BD - медиана.
Найти:∠ABD, ∠BAD, ∠ADB.
Решение:Так как △АВС - равнобедренный => BD - медиана, высота, биссектриса.
Так как BD - биссектриса => ∠ABD = ∠CBD = 80˚/2 = 40˚
△АВС - равнобедренный => ∠А (он же BAD) = ∠С
Сумма углов треугольника равна 180°.
=> 180° - 80° = 100˚ - сумма ∠С и ∠А (BAD)
∠А (BAD) = ∠С = 100°/2 = 50°
Сумма углов треугольника равна 180°.
Так как BD - высота => ∠ADB = 90˚
ответ: 40°, 50°, 90°.