
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
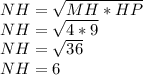
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
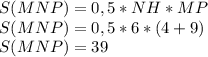
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
Половина основания b/2=а*cos(30)=a*sqr(3)/2, b=a*sqr(3)
Известно, что:
R=a^2/sqr(4a^2-b^2)
Подставив значение b, получим: R=a
Отсюда: АВ=2 см
Во второй задаче центр вписанной окружности совпадает с точкой пересечения биссектрис, поскольку радиусы опущенные из центра в точки М, Т и Р, образуют пары равных прямоугольных треугольников (ВОМ и ВОТ и т.д.). Четырехугольник РОТС является квадратом, так как радиусы проведены в точки касания и перпендикулярны катетам. По условия диагональ этого квадрата равна корень из 8, следовательно сторона будет в корень из двух раз меньше, отсюда:
r=sqr(8/2)=2 Угол ТОР=90 град. Угол ТМР является вписанным, он измеряется половиной дуги, на которую опирается. Дуга составляет 90 градусов, так как ограничена точками Р и Т, а угол РСТ прямой. Следовательно угол ТМР=45 град.