Через три точки можно провести плоскость.⇒
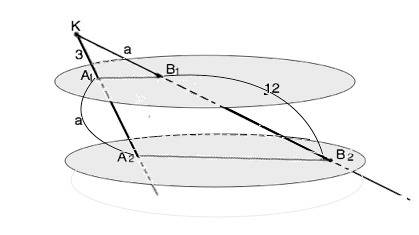
Все точки прямых КА2 и КВ2 лежат в одной плоскости. Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны. ⇒А1В1|║А2В2.
Треугольники КА2В2 и КА1В1 подобны по равным углам.
Из подобия следует
КА2:КА1=КВ2:КВ1
Обозначим А1А2=КВ1=а
Тогда (а+3):а=(а+12):а ⇒
а²=36, а=√36=6 см
КА2=КА1+А1А2=9 см
Пусть основание равнобедренного треугольника равно 3х, тогда боковые стороны пусть равны 4х и 4х.
Периметр - сумма длин всех сторон.
Составим линейное уравнение и решим его -
3х+4х+4х = 88 см
11х = 88 см
х = 8 см.
Основание = 3х = 3*8 см = 24 см.
Боковые стороны = 4х = 4*8 см = 32 см.
ответ: 24 см, 32 см, 32 см.