исходя из этих данных можно решить только в случае, если исходный треугольник мре - равнобедренный, с равными сторонами мр и ре.тогда все легко.ра - является в данном случае и биссекриссой и высотой.и у нас 2 прямоугольных треугольника мра и аре, в которых ма=ае=в/2 (т.к. высота в равнобедренном треугольнике делит основание пополам).собствено дальше все решение основано на свойствах прямог. треугольника, а именно.мр - это гипотенуза мра, и равнамр = ма * синус (бетта/2)=в/2 *синус (бетта/2)а ра - это катет того же прямоуг треугольника, и он равен ра=ма/тангенс (бетта/2)=в/2 / тангенс (бетта/2)
но если треугольник мре - произвольный, то боюсь решить не получится, хотя мне кажется он все-таки равнобедренный.удачи
1.
Синус угла A — равен: AB/CB.
Так как угол нам уже известен(42°), то его синус найдём по таблице: 0,6691.
Тоесть — катет CB равен: 0.6691*8 = 5.353.
Катет AC — найдём по теореме Пифагора: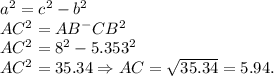
Вывод: AC = 5.94; CB = 5.353.
2.
Второй катет равен(по теореме Пифагора):
Второй катет равен: 12.7.
Найдём углы по их тангенсам.
Тангенс угла А равен: противоположный катет делить на прилежащий катет.
У нас есть треугольник ABC(прямой угол — C), по нашим расчётам — AB = 15; AC = 8; BC = 12.7.
Вывод: <B = 33°; <A = 57°.
3.
<M = 70° => <K = 90-70 = 20°.
Формула вычисления катета, зная гипотенузу, и угол прилежащего катета таков:
Гипотенузу найдём по теореме Пифагора: