ответ: ∠АСВ = 112°
Объяснение:
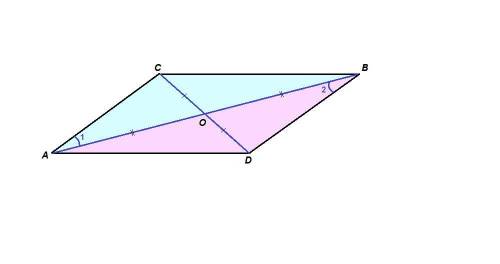
1. АО = ОВ и CO = OD по условию,
∠АОС = ∠BOD как вертикальные, значит
ΔАОС = ΔBOD по двум сторонам и углу между ними.
Из равенства треугольников следует, что
АС = BD и ∠САО = ∠DBO.
2. Тогда в треугольниках АСВ и BDA:
АС = BD, ∠1 = ∠2, AB - общая сторона, значит
ΔАСВ = ΔBDA по двум сторонам и углу между ними.
3. ∠1 = ∠2, а эти углы - накрест лежащие при пересечении прямых АС и BD секущей АВ, значит
АС║BD.
∠АСВ + ∠CBD = 180°, так как эти углы соответственные при пересечении параллельных прямых АС и BD секущей ВС, тогда
∠АСВ = 180° - ∠CBD = 180° - 68° = 112°
ответ: Р=7,52
Объяснение: найдём стороны треугольника АВ, ВС, АС по формуле:
АВ=√((х1-х2)²+(у1-у2)²+(z1-z2)²)
АВ=√((1,5-2)²+(1-2)²+(0-(-3))²=
=√(-0,5)²+(-1)²+3²)=√(0,25+1+9)=√10,25
AB=√10,25≈3,2
По этой же формуле найдём остальные стороны:
ВС=√((2-2)²+(2-0)²+(-3-(-1))²=
=√(2²+(-3+1)²)=√(4+(–2)²)=√(4+4)=√8=2√2
ВС=2√2≈2×1,41=2,82
АС=√((1,5-2)²+(1-0)²+(0+1)²)=
=√((-0,5)²+1+1)=√(0,25+1+1)=√2,25=1,5
АС=1,5
√10,25≈3,2;
2√2≈2×1,41=2,82
Теперь найдём периметр треугольника зная его стороны:
Р=АВ+ВС+АС=√10,25+2√2+1,5=
=3,2+2,82+1,5=7,52
Р=7,52