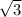площадь полной поверхности призмы будет равна: 126√3.
В произвольном выпуклом четырехугольнике - такой четырехугольник с вершинами в серединах сторон - параллелограмм, поскольку противоположные стороны являются средними линиями в треугольниках, образованных боковыми сторонами и диагоналями. Поэтому стороны этого четырехугольника параллельны диагоналям исходного четырехугольника, и - важно! - равны половинам диагоналей (ну, скажем, стороны 1 и 3 параллельны одной диагонали исходного четырехугольника и равны её половине, а стороны 2 и 4 - другой).
Остается сказать, что в равнобедренной трапеции диагонали равны. Следовательно, равны соседние стороны рассмотриваемого параллелограмма - они равны половине диагоналей. Поэтому он - ромб.
(Полупустой стакан равен полуполному. Поэтому пустой стакан равен полному :)))
Объяснение:
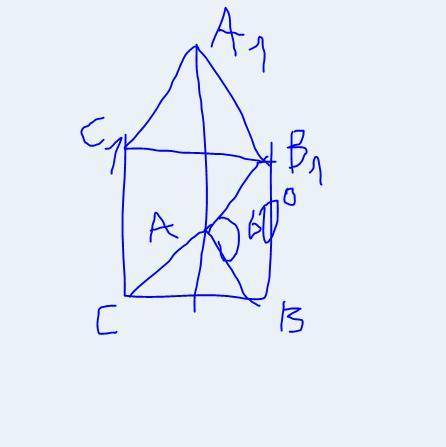
a) Ромб - параллелограмм, у которого все стороны равны, а углы непрямые.
Рассмотрим ∆DAB:
LF - средняя линия треугольника, т.к AF=FB и AL=LD => LF // DB
Рассмотрим ∆BCD:
NK - средняя линия треугольника по таким же признакам, и NK // DB => и // LF.
В ∆ABC и ∆ADC FK // AC // LN по таким же признакам.
Мы знаем, что средняя линия треугольника равна половине основания этого треугольника, и по свойствам прямоугольника: AC=DB => и FK=KN=NL=LF
=> FKNL - ромб по определению. Ч.Т.Д.
б) мы можем свободно использовать равнобедренную трапецию, у которой диагонали равны, => доказательство соответствует пункту a)
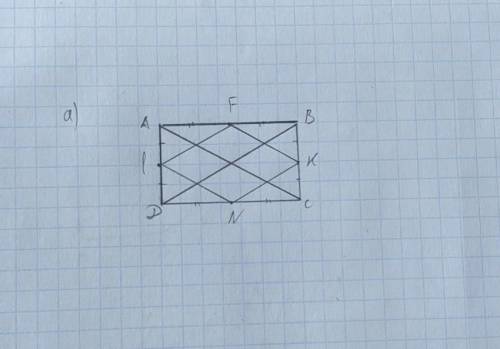
126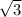
Объяснение:
Высота призмы BB1=AB1*sin60=12*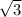
/2=6
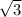
Сторона основания AB=AB1*cos60=12*1/2=6
Площадь боковых сторон равна 3*6*6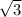
=108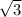
Площадь основний равна 2*6^2*/4=18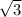
(Формула площади равностороннего треугольника)
Площадь полной поверхности равна (18+108)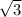
=126