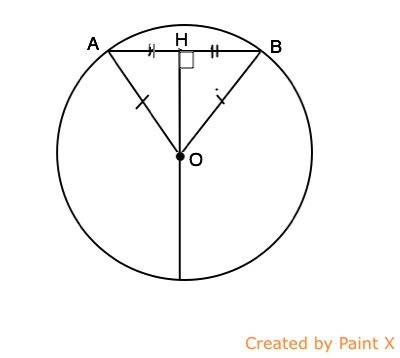
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Объяснение:
площадь боковой поверхности призмы
S=4см²
найти площадь диагонального сечения призмы
сперва находим длину ребер призмы
формула площади боковой поверхности призмы
выглядит так
Sбок=Р×h , Р=4a периметр основания правильной четырехугольной призмы , h высота призмы .
пусть длина ребра основания будет а=1см
тогда Р=4а=4×1=4см
высота h=Sбок/Р=4/4=1см
из этого выходит что грани призмы квадратные.
диагональ квадрата равна dкв=а√2
можно проверить через теорему Пифагора
dкв=√а²+а²=√1²+1²=√1+1=√2 см
Площадь диагонального сечения призмы составляет
Sд.с=d×h= √2 ×1=√2 см²