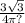
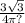
15
Объяснение:
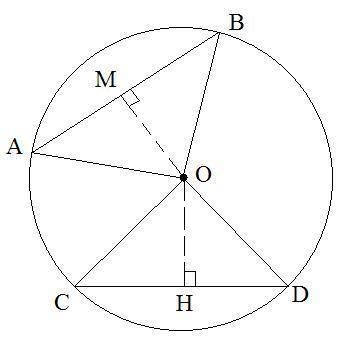
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15
15
Объяснение:
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15

ответ: а) 6/π
Пусть H – высота конуса и высота пирамиды, R – радиус основания конуса и радиус описанной около основания пирамиды окружности. Найдем отношение объема вписанной пирамиды к объему конуса.
Объём конуса, и объём пирамиды вычисляются по формуле:
V = 1/3 Sосн·Н
Так как в основании конуса – круг, то Sосн. конуса = πR²
Так как по условию четырехугольная пирамида правильная, то в основании – квадрат, следовательно Sосн. пирамиды = а²
Vп/Vк = 1/3 а²H / 1/3πR²H = а² / πR²
Площадь квадрата равна половине квадрата длины его диагонали:
S = d²/2, d = 2R, S = (2R)²/2 = 2R², тогда:
Vп/Vк = а² / πR² = 2R² / πR² = 2/π
Так как по условию задачи объём конуса равен 3, то Vп/3 = 2/π, Vп = 6/π
ответ: 6/π