6) Хорды AB и CD пересекаются в точке E, тогда верно равенство
АE·BE=CE·DE
7) Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14) X Источник информации , r – радиус окружности, d – диаметр окружности.
8) Формула для вычисления площади круга
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415). 2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
9)Окружность называется вписанной в треугольник, если она касается всех его сторон. Окружность называется описанной около треугольника, если она проходит через все его вершины. Теорема 1. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Дано: ∆MNP, ∆FPN – прямоугольные, МР ∩ NF= К, MN = FP.
Докажите: ∆NKP – равнобедренный.
Доказательство:
Рассмотрим Δ MNP и ΔFPN . У них MN = FP по условию, NP– общая сторона, значит Δ MNP = ΔFPN по признаку равенства прямоугольных треугольников, следовательно, ∠MPN = ∠FNР , значит, ∆ NKP – равнобедренный по признаку равнобедренного треугольника о равенстве углов при основании. Чтд.
О какой общей стороне идёт речь в решении этой задачи?- NP– общая сторона, является катетом в прямоугольных треугольниках ∆MNP и ∆FPN .
Приравняем данные функции и решим полученное квадратное уравнение:
По формуле Ньютона-Лейбница найдём площадь:
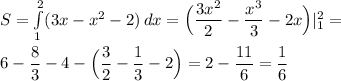
ответ: