ответ:32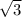
Объяснение: так там угол в 60 а сумма дополнительных углов 180 то соседний равен <CDA= 120 и так это ромб <ВAD=60 градусам так как диагональ BD делит углы B и D пополам а так же делит на два равносторонних треугольника BAD и BCD то диагональ BD равна 8 , теперь вычислим площадь ромба по формуле ab*sinL так как стороны равны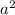 
sinL не важно какой угол мы возьмем sin120 или sin 60 они равны но если вы не формулу суммы углов то лучше использовать sin60 и мы вычисляем 
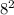*sin60= 
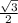*64= 32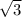
Геометрия - это наука , изучающая свойства фигур.
Геометрическая фигура (тело) – абстрактный предмет, в котором рассматривается только форма и размер, не обращая внимания на физические свойства.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия.
Прямая и плоскость безграничны, поэтому на чертеже изображают часть.
Прямые обозначают двумя заглавными латинскими буквами, соответствующим двум точкам на прямой, или одной малой буквой.
Точки обозначают заглавными латинскими буквами.
Знак begin mathsize 12px style element of end style означает принадлежание, т.е. begin mathsize 12px style A subscript 1 element of m end style означает, что точка А1 принадлежит прямой m или лежит на ней. И begin mathsize 12px style A subscript 2 not an element of m end style соответственно, не принадлежит или не лежит.
Точка — это абстрактный предмет, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Прямая А В
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Отрезок изображается так:
Отрезок
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Луч
Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.
Дополнительные лучи
Плоскость, как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
расстояние от центра сферы до плоскости сечения
L=2√7 см
Объяснение:
линия пересечения сферы это длина окружности данного сечения
Ссеч=12π см
диаметр сферы Dc=16см
радиус сферы R=Dc/2=16/2=8см
найти расстояние от центра сферы до плоскости сечения L - ?
расстояние от центра сферы до плоскости сечения , это самое короткое расстояние которое перпендикулярно к плоскости сечения.
и образует прямой угол .
возмем некоторою точку М лежащего на окружности этого сечения, расстояние от точки до центра О1 сечения будет радиусом сечения r.
А от точки М до центра О сферы радиусом сферы R=8см
выходит прямоугольный треугольник Δ ОМО1
где МО=R=8 гипотенуза,
ОО1 = L и МО1=rсеч катеты
находим радиус сечения rсеч=MO1
длина окружности сечения составляет Ссеч=12π см
формула окружности выглядит так
С=πD=2πr отсюда радиус r=С/2π
rсеч=МО1= Ссеч/2π=12π/2π=6 см
расстояние между плоскостью сечения и центром сферы находим по теореме Пифагора
L=OO1=√R²-rcеч²=√МО² - МО1² =
=√8² - 6²=√64-36=√28=√4×7=2√7 см