Question

1)Дан треугольник со сторонами 20 см, 34 см и 42 см.Данная точка P находится на расстоянии 25 см от всех сторон треугольника. Найти расстояние от точки P до плоскости треугольника. 2)Дан треугольник со сторонами 39 см ,17 см ,28 см. Точка S находится на расстоянии 6 см от плоскости треугольника и на одинаковом расстоянии от его вершин.Найдите расстояние от S до вершин треугольника.
РЕШИТЬ ХОТЬ 1 ЗАДАЧУ

Answer 1

24 см

Объяснение:

1)   Пусть РО - расстояние от точки Р до плоскости (т.О ∈ плоскости, РО - высота пирамиды). Поскольку точка P находится на расстоянии 25 см от всех сторон треугольника, то т. О - центр круга, впис. в треугольник (r).

р=(20+34+42)/2=48

по формуле Герона S =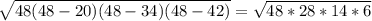 $\sqrt{48(48-20)(48-34)(48-42)} =\sqrt{48*28*14*6}$=$\sqrt{16*3*7*4**7*2*3*2}=4*3*7*2*2=336$ cм²

r=S/p,   r=336/48= 7 см

За т. Пифагора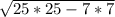 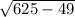$\sqrt{25*25-7*7}$=$\sqrt{625-49}$=24 см

2) Поскольку т. S находится на одинаковом расстоянии от вершин треугольника, то т.О - центр круга, опис. навк.треугольника.

Далее аналогично: найти р = 42 , потом S по формуле Герона  (S = 210), а потом  найти R = 39*28*17/4*210=22,1

Далее использовать т. Пифагора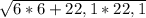 $\sqrt{6*6+22,1*22,1}$=22,9