Нам известны все 3 измерения прямоугольного параллелепипеда, значит мы можем найти его диагональ.
a, b, c - его различные рёбра; d - его диагональ.
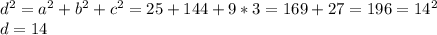
ответ: 14 см.
Если 3√3 выражен в см.
Доказательство этой формулы:
Все грани прямоугольного параллелепипеда прямоугольники, это определение. Поэтому квадрат диагонали основания будет равен a²+b². Рассмотрим плоскость в которой есть диагональ параллелепипеда и наша диагональ прямоугольника из основания. Это плоскость образует сечение, которое является прямоугольником т.к. боковые рёбра перпендикулярны основанию, а наша диагональ прямоугольника лежит именно в основании. Так вот одна сторона прямоугольника это боковое ребро, а вторая это диагональ, которую мы искали вначале. При этом диагональ этого прямоугольника и является диагональю параллелепипеда, то есть d²=c²+(a²+b²), т.к. это прямоугольник. Что и требовалось доказать.
Смотри на рисунок, для понятности.

конус.
V = 270п см^3
h = 10 см
Найти:R - ?
Решение:V = 1/3 * пR² * h = 270
V = 1/3 * пR² * 10 = 270
Составим уравнение и решим его:
Число "п" в уравнении нам не нужно, так как при вычислении объёма, видно, что его не вычисляли. (270п см²)
Пусть х - радиус R.
1/3 * x² * 10 = 270
1/3x² = 270
x² = 81
x = +9; -9
Возможные решения: 9; -9.
Но так как единицы измерения не могут быть отрицательными => х = 9
Итак, R = 9 см
ответ: 9 см.