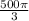 .
.Две сферы.
V = 500п/3 ед. кб.
d = 10 ед.
Найти:V - ?
Решение:R1 - радиус первой сферы.
R2 - радиус второй сферы.
Составим уравнение, с которого узнаем, чему равен радиус R1
Пусть х - радиус R1
V сферы = 4/3пR^3 = 500п/3
В уравнении число п нам не нужно, так как при вычислении объёма сферы, видео, что число п не вычислялось:
4/3 * х^3 = 500/3
х^3 = 125
х^3 = 5^3
х = 5
Итак, R = 5 см
Так как d = 10 см => R1 = R2 = 5 см, так как R1 + R2 = 5 + 5 = 10 см
Из этого =>, что две сферы касаются внешним образом.
=> сферы образуют одну общую точку, но они не образуют никакой фигуры, то есть V = 0
ответ: 0Если диагонали четырёхоугольника перпендикулярны, то этот четырёхугольник - ромб, а значит, все его стороны равны, т.е. АВ=ВС=СD=АD=а.
Если этот ромб вписали в окружность, то он-правильный. А правильный ромб-это квадрат.
Значит, АВСD-квадрат.
Точка О является центром окружности.
Также она является серединой пересечения диагоналей.
По теореме Пифагора находим, что ОВ= а*корень из 2 и всё поделить на 2
Пусть ОН-расстояние от точки О до стороны АВ. ВН=половине АВ= а\2
Находим ОН. Также по теореме Пифагора.
ОН= а\2
V=0.
Пересечением двух сфер является точка, т.е.
взаимное расположение сфер таково, что
они касаются.
Объяснение:
V=4/3piR^3
По условию V=500pi/3 ,
следовательно: 4/3рiR^3=500pi/3
4R^3=500
R^3=125
R=5.
Расстоянме между центрами сфер :
5+5=10 - сферы не пересекаются, а имеют
лишь точку внешнего касания.