Все грани прямоугольного параллелепипеда - прямоугольники.
Двугранный угол DABD₁ - это угол между плоскостями DAB и ABD₁.
АВ - ребро двугранного угла.
DA⊥AB как стороны квадрата,
DA - проекция наклонной D₁A на плоскость DAB, значит
D₁A⊥АВ по теореме о трех перпендикулярах.
DA⊥AB и D₁A⊥АВ,, значит ∠D₁AD - линейный угол двугранного угла D₁ABD.
ΔADC: ∠ADC = 90°, по теореме Пифагора
AD = √(AC² - CD²) = √(100 - 36) = √64 = 8 дм
ΔD₁AD: ∠D₁DA = 90°, DD₁ = AA₁ = 8√3 дм, AD = 8 дм,
tg∠D₁AD = D₁D / AD = 8√3 / 8 = √3
∠D₁AD = 60°
Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
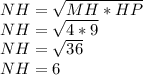
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
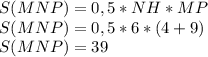
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
Объяснение:
1дано
Цилиндр
R=4cm
H=10cm
Sпол.=?
Решение
Sпол.=2πR(H+R)
Sпол.=2*4π(10+4)=8π*14=112π см²
π≈3,14
Sпол.=112*3,14=351,68 см²
ответ полная Площадь цилиндра равно 351,68
3)
Дано
Цилиндр
R=2cm
L=6cm
V=?
Решение
V=πR²L
V=2²*6π=4*6π=24π cm³
π≈3,14
V=24*3,14=75,36 cm³
ответ: объем цилиндра равен 75,36 см³
2) при условии что диагональ сечения 15
Дано
Цилиндр
D=15cm диагональ сечения
R=3cm радиус окружности
H=?
Решение
Диаметр окружности равен двум радиусам d окр.=2R
d окр.=3*2=6см
По теореме Пифагора найдем высоту
Н²=D²-d окр.
Н=√(15²-6²)=√(225-36)=√189=3√21
ответ: высота цилиндра равная 3√21