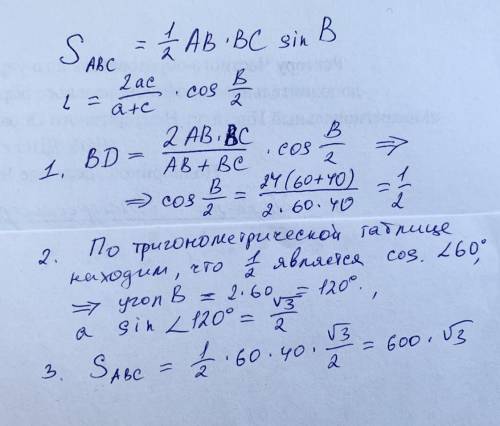
Треугольник АВС, О -центр, ОН радиус перпендикулярный АВ в точке касания, ОК радиус перпендикулярный АС в точке касания,
четырехугольник АНОК, угол АНО+углуАКО=90, уголА=60, угол НОК = 360-90-90-60=120
треугольник НОК равнобедренный ОН=ОК=радиусу=1, проводим высоту ОР на НК, угол ОНК=углуОКН=(180-120)/2=30, треугольник ОКР прямоугольный, ОР=1/2 ОК - лежит напротив угла 30, ОР = 1/2=0,5, НР=РК= корень (ОК в квадрате - ОР в квадрате) =
=корень( 1-0,25) = 0,5 х корень3, НК =НР+РК= 2 х 0,5 х корень3 =корень3
треугольник АНК равнобедренный АН=АК как касательные к окружности. проведенные из одной точки, угол АНК=углуАКН = (180-60)/2=60, треугольник АНК равносторонний углы=60, значит АК=АН=НК=корень3
расстояние=корень3
Когда все это нарисовали, то видим, что имеем вписанный четырехугольник. Но четырехугольник может быть вписпнным только и только тогда, когда сумма противоположных углов равна 180°.
Но углы АВС и АDС опираются на диаметр, значит равны по 90°, а в треугольниках АОD
и АОВ (О-центр круга) все углы равны, так как треугольник равносторонний (все стороны - радиус)
т.е угол САD=уголВDС= 60° и следовательно угол ВАD = 120°
Тогда противоположный угол ВСD = 180°-120°=60°. Все углы найдены.
А градусные меры дуг равны удвоенному значению угла, на эту дугу опирающегося, то есть
Дуга АВ = АD = 60° дуга ВС = СD = 120°
итого 120+240=360° - это проверка
ответ: C)
600√3
Решение: S=1/2 *AB*BC* sin B
а длина биссектрисы через две стороны и угол между ними;
ВД= (2АВ*ВС* cоs (∠В/2) /(АВ+ВС).
cоs (∠В/2) =ВД*(АВ+ВС)/2АВ*ВС=24*(60+40)/2*60*40=12/24=1/2.
∠В/2=60°
∠В=120°
sin120°=√3/2
S=1/2*60*40*√3/2=600√3