Объяснение:
Раз нам даны точки в пространстве, то скорее всего с векторами уже знакомы, тогда. Найдем векторы АВ и ВС, для этого нужно от координат конца отнять соответствующие координаты начала, тогда
(в)АВ(-5-2;4-5;-4-(-1))=(-7;-1;-3)
(в)BC(1-(-5);-2-4;2-(-4))=(6,-6,6)
По определению параллелограма это четырехугольник у которого 2 пары параллельных равных сторон, сделовательно (в)AB=(в)CD
(в)AB(-7;-1;-3), C(1;-2;2) Пусть точка D имеет координаты x,y,z. Следовательно (в)CD(x-1;y+2;z-2) и эти выражения x-1;y+2;z-2 соответственно равны -7;-1;-3. Тогда
x-1=-7⇔x=-6
y+2=-1⇔y=-3
z-2=-3⇔z=-1. Следовательно координаты точки D(-6,-3,-1)
Так как диагональ точкой пересечения делится пополам, то точка пересечения диагоналей это середина диагонали, диагональ - отрезок соединяющий 2 несоседние вершины, значит найдем середину BD или АС
Координаты середины отрезка находятся по формуле среднего арифмитеческого соответствующих координат концов, т.е. абсцисса первой точки+ абсцисса второй точки делить на 2, ордината и апликата соответственно, тогда
Середина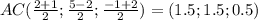 
Точка с этими координатами,пусть точка О, и есть точка пересечения диагоналей.
Длина AB .длина вектора это есть квадратный корень из суммы квадратов его координат, тогда длина АВ = длине вектора АВ
|(в)АВ|=
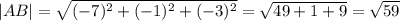
пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две прямые параллельны. Свойство - если мы уверены в справедливости суждения, мы формулируем свойство объекта. Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.