ответ: S = 324 см^2
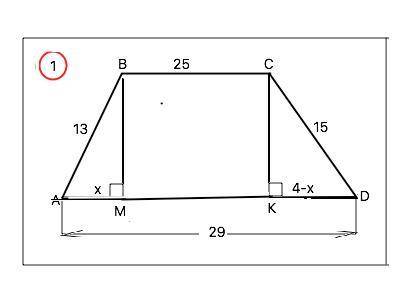
Решение: проведем высоты BH и CK на основание AD(они равны). У нас получился прямоугольник BCKH. Пусть x=AH, тогда KD = AD-HK-x = 4-x. BH^2= AB^2-x^2 = 225-x^2, CK^2 = 13^2-(4-x)^2
BH = CK => BH^2=CK^2
225-x^2=13^2-(4-x)^2= 169-16+8x-x^2= 153+8x-x^2
72 = 8x
x = 9(см)-AH
BH^2= 225-81 = 144
BH=12 см
SABCD = 1/2*h*(BC+AD) = 1/2*12*54 = 324 см^2.
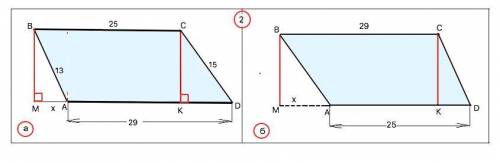
Можно было провести из угла B прямую, параллельную BD, у нас бы получился параллелограмм, далее находим площадь треугольника по формуле Герона, далее значение площади тр-ника приравниваем к обычной формуле площади тр-ника и находим высоту(12см), а потом находим площадь самой трапеции.
Все окружности подобны, ⇒ отношение их радиусов равно отношению их длин. ⇒ R=2/3•r√3 или R=2r/√3 . Радиусом окружности, вписанной в правильный многоугольник, является его апофема ( так называется отрезок, проведенный из центра правильного многоугольника перпендикулярно стороне). На рисунке приложения нарисован равнобедренный треугольник, боковые стороны которого – радиусы описанной окружности, высота – радиус вписанной окружности, основание – сторона данного многоугольника. ОН - высота и медиана равнобедренного треугольника. АН=ВН. sin∠OBН=ОН:ОВ=r:R=r:2r/√3=√3/2 ⇒ углы при основании равнобедренного ∆ АОВ=60°. ⇒ угол АОВ=60°. Полная окружность содержит 360°, поэтому сторон у данного по условию многоугольника 360°:60°=6. АВ=12:6=2 Формула площади правильного треугольника S=a²√3:4. Правильный шестиугольник можно разделить на 6 правильных треугольников, поэтому его площадь равна 6•AB²•√3/4=6√3 (ед. площади)