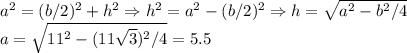5,5
Объяснение:
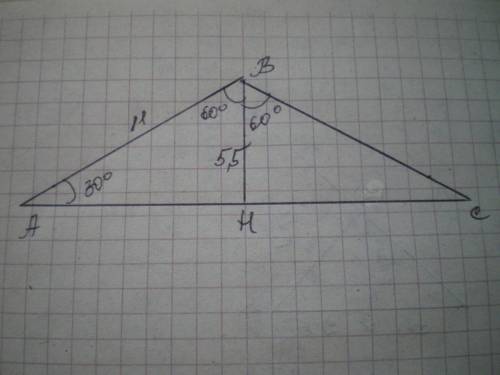
Высота равнобедренного треугольника является биссектрисой, поэтому ∠АВН=СВН=120:2=60°.
ΔАВН - прямоугольный, ∠А=90-60=30°, т.к. сумма острых углов прямоугольного треугольника составляет 90°.
ВН=1/2 АВ, т.к. лежит против угла 30°, ВН=5,5 .
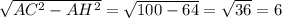 см;
см;
5.5
Объяснение:
Пусть боковые стороны будут , а основание -
, а основание - 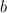
По теореме косинусов: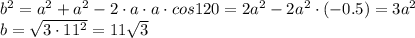
Опустим высоту, тогда получится прямоугольный треугольник со сторонами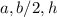 (боковая сторона изначального треугольника, половина основания (т.к. высота ещё является и медианой) и сама высота).
(боковая сторона изначального треугольника, половина основания (т.к. высота ещё является и медианой) и сама высота).
Тогда по теореме Пифагора: