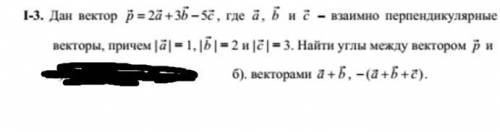
Три прямые, пересекающиеся попарно, образуют три точки пересечения.
а) Через три точки, не лежащие на одной прямой, можно провести плоскость, притом только одну.
Следовательно, любая прямая, пересекающая прямые a и b,
но не проходящие через точку С, будет лежать в той же плоскости, что прямые а и b.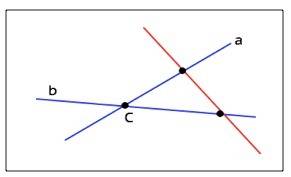
Объяснение:
Угол между векторами определяется через их скалярное произведение:
Выражаем отсюда косинусы:
Считаем скалярные произведения и модули:
(нулевые скалярные произведения в следствие перпендикулярности векторов). Аналогично:
Подставляем в косинусы: