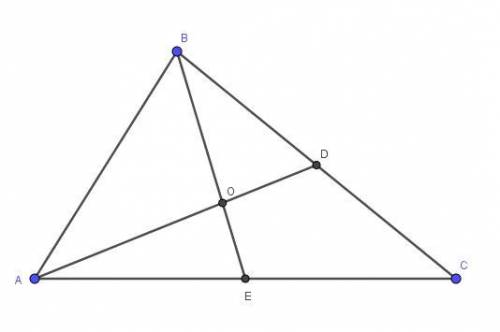
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть 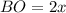 см и
см и 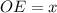 см, тогда
см, тогда 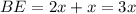 , что по условию он равен 9 см.
, что по условию он равен 9 см.
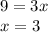
Следовательно, 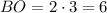 см и
см и 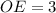 см
см
Аналогично, пусть теперь 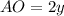 см и
см и 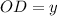 , тогда
, тогда 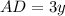 и по условию равен 12 см
и по условию равен 12 см
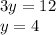
Таким образом, 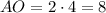 см и
см и 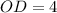 см.
см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника 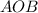
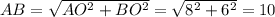 см
см
По теореме Пифагора из прямоугольного треугольника 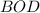
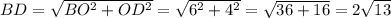 см
см
Тогда 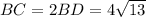 см
см
Из прямоугольного треугольника 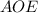 по теореме Пифагора
по теореме Пифагора
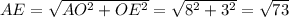 см
см
Тогда 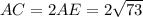 см
см
ответ: 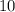 см;
см; 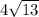 см;
см; 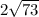 см.
см.
1.1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.
2.Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону. В зависимости от типа треугольника высота может содержаться внутри треугольника, совпадать с его стороной или проходить вне треугольника у тупоугольного треугольника.
3.Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r. Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
4.Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно. Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом.
5.Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон.
6.а — основание, 6 — боковая; а = b + 5; а + 2b = = b + 5 + b + b = 3b + 5 = 35; 3b = 30; b = 10, а = 10 + 5 = 15.
1 неверно, так как косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе
3 неверно, так как площать парллелограмма равна произведению длин его смежных сторон на синус угла между ними.
4 неверно, так как сумма углов треугольника равна 180 градусов, а других ограничений на углы треугольника нет.